Question 1203598: How many permutations of the letters {A, B, C , D, E , F , G } are
there, such that
1 A precedes B
2 A precedes B, and C precedes D
3 A precedes B, and B precedes C
4 C,D,E appear together in this order
5 A,B are appear together in this order, as do C , D
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20067)   (Show Source): (Show Source):
You can put this solution on YOUR website! How many permutations of the letters {A, B, C , D, E , F , G } are
there, such that
1 A precedes BThat's the number of permutations of these 6 things AB, C, D, E, F, G
taken all 6 at a time. 2 A precedes B, and C precedes DThat's the number of permutations of these 5 things AB, CD, E, F, G
taken all 5 at a time. 3 A precedes B, and B precedes CThat's the number of permutations of these 5 things ABC, D, E, F, G
taken all 5 at a time. 4 C,D,E appear together in this order
That's the number of permutations of these 5 things A, B, CDE, F, G
taken all 5 at a time. 5 A,B appear together in this order, as do C,D.
That's the number of permutations of these 5 things AB, CD, E, F, G
taken all 5 at a time.
You can calculate all these numbers of permutations yourself. They're just
factorials.
Edwin
Answer by ikleyn(52954)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many permutations of the letters {A, B, C , D, E , F , G} are
there, such that
1 A precedes B
2 A precedes B, and C precedes D
3 A precedes B, and B precedes C
4 C,D,E appear together in this order
5 A,B  appear together in this order, as do C,D appear together in this order, as do C,D
~~~~~~~~~~~~~~~~~~~~~~~~
My reading and understanding is different from that of Edwin,
so my solutions and my answers are different.
(1) A precedes B
In English, "A precedes B" means that A goes/comes before B, but it is not necessary
that B goes/comes immediately after A: it may happen that there is / (there are) other letter / (letters)
after A, but before B. In other words, "A precedes B" means that A goes/comes before B,
but A and B are not necessary adjacent (= not necessary appear altogether).
Based on this understanding, there are 7! = 7*6*5*4*3*2*1 = 5040 permutations of 7 letters
{A, B, C , D, E , F , G}; of them, in exactly half cases, A precedes B. In other half,
in opposite, B precedes A. To convince yourself that it is true, take any permutation
where A precedes B and make swap.
So, the ANSWER to (1) is 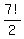 = = 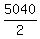 = 2520. = 2520.
(2) A precedes B, and C precedes D
As we just learned from (a), there are 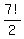 = = 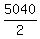 = 2520 permutations
of 7 letters {A, B, C , D, E , F , G}, such that A precedes B.
Of them, in half cases C precedes D; in other half cases D precedes C.
So, the ANSWER for (2) is = 2520 permutations
of 7 letters {A, B, C , D, E , F , G}, such that A precedes B.
Of them, in half cases C precedes D; in other half cases D precedes C.
So, the ANSWER for (2) is 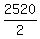 = 1260. Or, which is the same, = 1260. Or, which is the same, 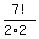 = =  . .
(3) A precedes B, and B precedes C
With any permutation of 7 letters {A, B, C , D, E , F , G }, there are 3!-1 = 6-1 = 5 other permutations
where letters A, B and C are swapped in their positions.
It gives you an idea, that with any favorable permutation, where A precedes B and B precedes C, there are 5 other
permutations with swapped A, B and C in their positions.
So, the answer to (c) is 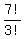 = = 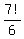 = = 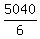 = 840. = 840.
(4) C,D,E appear together in this order.
For this part, I agree with Edwin.
(5) A,B appear together in this order, as do C , D
In this part, formulation in the post is unclear (= does not sound harmonically *) and needs to be clarified.
May be, you want to ask "A,B appear together in the same order, as do C,D"
Then it is clear, but it is DIFFERENT from your original formulation.
Having unclear formulation, I prefer do not touch this part.
Solved (to that extent as possible).
-------------------
*) In Math, if a problem does not sound harmonically, it is a sure sign that it is formulated incorrectly.
Why ? - Because harmony is the hidden meaning of Math.
|
|
|