Question 1203274: (a) In how many different ways can the letters in the word
ARRANGEMENTS be arranged?
(b) Find the number of ways the arrangement begins with the letters EE.
Found 2 solutions by math_helper, ikleyn:
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website!
a) There are 12 letters, and if these were all unique, there would be 12! unique ways to arrange them. However, we must divide out the duplicate (non-distinct) arrangements. For this, we note there are 2 A's, 2 R's, 2 N's, and 2 E's, each of which contributes 2! non-distinct arrangements:
Number of unique arrangements = 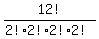 = 29937600 = 29937600
Part (b) can be done similarly. Since the arrangements begin with EE, that effectively leaves 10 letters to arrange, and you'll need to remove duplicates in a similar way as in part (a). It is as if the E's are removed and you repeat part (a) without the E's.
Hint: the answer will be 10! / (something)
Answer by ikleyn(52943)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
To tutor @math_helper
Dear tutor @math_helper
If you open your post with < pre >,
then you should CLOSE the post with the symbols < / pre >, for accuracy.
In addition to accuracy, it makes an influence at the appearance of your post.
Suddenly, you will discover that the appearance becomes to be manageable (!), in a way as you expect it (!!)
Best regards
@ikleyn
|
|
|