SOLUTION: The letters of the word PROBABILITY are arranged at random. Find the number of arrangements where the two Is are separated.

Algebra ->  Permutations -> SOLUTION: The letters of the word PROBABILITY are arranged at random. Find the number of arrangements where the two Is are separated.      Log On


   

Question 1203273: The letters of the word PROBABILITY are arranged at random. Find the number of arrangements where the two Is are separated.
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


The comment from tutor @ikleyn is correct. In counting the number of arrangements with the two I's together, there is only one way to arrange those two I's, because they are the same letter.

The total number of arrangements is of 11 letters including 2 pairs. That number is %2811%21%29%2F%28%282%21%29%282%21%29%29

For the number of arrangements with the 2 I's together, treat them as a single unit.

-------------------------------------------

NO!... Then there are 10 items with one (other) pair; and the two I's in the unit can be arranged in either of 2 orders. This number is then %282%29%28%2810%21%29%2F%282%21%29%29

-------------------------------------------

Yes... Then there are 10 items with one (other) pair. the number of arrangements here is then %2810%21%29%2F%282%21%29

Subtract the second number from the first to get the number of arrangements in which the two I's are separated (i.e, not together).

You can do the actual calculations....

Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
The letters of the word PROBABILITY are arranged at random.
Find the number of arrangements where the two Is are separated.
~~~~~~~~~~~~~~~~~~~ 

The word PROBABILITY consists of 11 symbols.

Of them, two letters "B" make one repeating pair.
         Two letters "I" make another repeating pair.


The total number of all distinguishable arrangements of the word PROBABILITY is 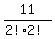11%2F%282%21%2A2%21%29 = 9,979,200.


Now let's calculate the number of all distinguishable arrangements of the word PROBABILITY
where two Is are together (are glued).

This pair of Is, placed together (glued), we can consider as one object.

Then we have arrangements of 10 = 11-1 objects with one repeating pair of Bs.

So, the number of all such distinguishable arrangements is 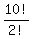10%21%2F2%21 = 1,814,400. 


Finally, the number of all distinguishable arrangements of the word PROBABILITY, where 
the two Is are separated is the difference


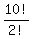    11%21%2F%282%21%2A2%21%29 - 10%21%2F2%21 = 9,979,200 - 1,814,400 = 8,164,800.


ANSWER.  The number of all distinguishable arrangements of the word PROBABILITY, where 
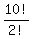         the two Is are separated is  11%21%2F%282%21%2A2%21%29 - 10%21%2F2%21 = 8,164,800.

Solved.

-------------------

The solution by tutor @greenestamps is incorrect.

In his solution, he correctly determined the number of all distinguishable arrangements
of the word PROBABILITY, but mistakenly highlight%28highlight%28doubled%29%29 the number of all distinguishable arrangements
of this word with two glued Is.


MEMORIZE: distinguishable arrangements are not the same as permutations !

Do not mix these two different conceptions - - - always DISTINCT them !


\\\\\\\\\\\\\\\\\\


If you want to see many other similar  (and different)  solved problems of this type,  look into the lesson
    - Arranging elements of sets containing indistinguishable elements
in this site.

Learn the subject from there.