SOLUTION: In a certain city, there are seven streets going north-south and five streets going east-west. How many street paths start at the southwest corner of the city, end at the northeast

Each such path is a combination of elementary 7 south->north parts/blocs and 
5 west->east parts/blocks, 7+5 = 12 blocks, in total.


So, using designation/letter V for south->north blocks ("vertical") and designation/letter H ("horizontal") 
for west->east blocks, each path can be coded as a word of 12 letters "V" and "H".


There is one-to-one correspondence between such paths and such words.


So, we can say that the number of paths equals the number of words of the length 12,
written using letter V and H.  Repeating of letters is allowed.


From Combinatorics, it is known that the number of such words is  

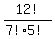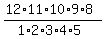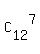     = after reduction of the fraction =  =  =  = 792.


Indeed, from the total 12 positions of the word, 7 positions for letters "V" can be selected 
in 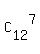   different ways; the rest 5 positions are occupied by the letters "H".


It gives us the answer to the problem's question: there are 792 such paths.

    How many distinguishable ways are there to place in line 7 red and 5 white balls, if they distinct only by color ?"