Question 1200860: Question: How many angles less than 180 degrees are formed by 12 straight lines which terminate in a point if no two of them are in the same straight line?
I have trouble understanding the question, despite reading it over and over again! Does it mean there are 12 straight lines are intersecting at one single point OR one end of the 12 lines are meeting at a point (12 lines radiating at a point)
Either answering or pointing to an illustrative question-number under Permutations and Combinations will be greatly appreciated.
Thank you
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If this problem came from your teacher, ask the teacher.
If it came from the other source, which you may ask, ask the source.
If it is found somewhere in the Internet, and you can not ask the source,
we are not responsible for it, since we do not control everything in the Internet.
If you can interpret it in a way to get interesting Math problem, (try to) do it.
If you can not, forget about this problem.
-----------------------
Actually, in Geometry, there is a standard name for a " straight line which terminates at one point ". This name is " a ray ".
A straight line, in the strict sense of Geometry, does not terminate anywhere - it is infinite in both directions.
Had I formulate this problem, I would do it in such a way that
only one interpretation be possible, as it should be for any true Math problem.
////////////////
Probably, they want to say that 12 different rays are released from one point on a plane.
After that, they want to ask, how many angles less than 180 degrees are formed.
If so, then each (unordered) pair of the rays form exactly one such angle,
and different angles are formed by different pairs of rays,
so the number of all such angles is 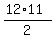 = 6*11 = 66, = 6*11 = 66,
exactly as the number of all different unordered pairs of the rays.
But it is my interpretation and reformulation, so I can not guarantee that they mean exactly the same.
I do not read in their minds.
|
|
|