Question 1197462: How many different professionals committees of 10 people can be formed, each containing at least 2 Professors, at least 3 Managers and 3 ICT Experts from list of 10 Professors, 6 Managers and 8 ICT Experts?
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many different professionals committees of 10 people can be formed,
each containing at least 2 Professors, at least 3 Managers and 3 ICT Experts
from list of 10 Professors, 6 Managers and 8 ICT Experts?
~~~~~~~~~~~~~~~~
Below in the Table, all possible different numbers of participanting members
are presented, satisfying the imposed conditions.
T A B L E
Professors Managers ICT experts Total
2 5 3 10
3 4 3 10
4 3 3 10
Now write the relevant formulas:
The number of different committees N(2P of 10, 5M from 6, 3E from 8) = 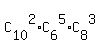 = 45 * 6 * 56 = 15120,
The number of different committees N(3P of 10, 4M from 6, 3E from 8) = = 45 * 6 * 56 = 15120,
The number of different committees N(3P of 10, 4M from 6, 3E from 8) = 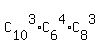 = 120 * 15 * 56 = 100800,
The number of different committees N(4P of 10, 3M from 6, 3E from 8) = = 120 * 15 * 56 = 100800,
The number of different committees N(4P of 10, 3M from 6, 3E from 8) = 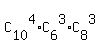 = 210 * 20 * 56 = 235200.
The total numbers of all possible committees is 15120 + 100800 + 235200 = 351120. ANSWER = 210 * 20 * 56 = 235200.
The total numbers of all possible committees is 15120 + 100800 + 235200 = 351120. ANSWER
Solved.
The solution is a simple and almost mechanical procedure.
The problem teaches you to organize your data, your thoughts and your calculations systematically.
|
|
|