Question 1197427: How many ways are there to distribute 15 district item into 5 distinct boxes with:
i) At least two empty box.
ii) No empty box.
Found 4 solutions by Edwin McCravy, greenestamps, ikleyn, rippletable:
Answer by Edwin McCravy(20054)   (Show Source):
You can put this solution on YOUR website! The words are not "district item". That makes absolutely no sense.
Copy it letter by letter just like it's written in your book or
on your computer screen, and maybe somebody will answer it. Don't
misspell or mistype anything. Read it carefully and edit it
before you post it.
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
The "stars and bars" method can be used to solve any problem like this involving distributing items into different groups.
Let's look at a simplified example of your problem where there are only 3 items and only 2 boxes.
It's easy to list the 4 possibilities for distributing 3 items into 2 boxes: 0 and 3, 1 and 2, 2 and 1, or 3 and 0.
Here is how to solve this example using stars and bars.
We start with 3 stars (*) to represent the 3 items:
***
To represent dividing the 3 items into 2 boxes, we use 1 bar (|) to represent a divider; note that to divide the items into n=2 groups, only n-1=1 divider is needed.
The different arrangements of the 3 stars and 1 bar represent the distinct ways of distributing the 3 items among the 2 boxes:
|*** --> 0 and 3
*|** --> 1 and 2
**|* --> 2 and 1
***| --> 3 and 0
With formal mathematics, the number of different ways to arrange a string of 4 symbols, of which 3 are the same and the other 1 is different, is calculated like this:
We will use this kind of calculation in finding the answers to your questions.
The basic problem in your post (without restrictions) is to find the number of ways of distributing 15 items into 5 boxes. Using stars and bars, we would have 15 stars and 5-1=4 bars, and the calculation would be
Now let's look at the two questions in your post.
The following analysis and solution are faulty. See farther down in my response for the correct solution.
The second one is actually easier, so we'll do that one first.
To make sure there are no empty boxes, we first put 1 item in each of the 5 boxes. That assures us that there will be no empty boxes, so there are no restrictions on where the remaining items go.
But that means we have to distribute 15-5=10 items into 5 boxes; the number of ways to do that is
ANSWER for your second question: 1001 ways to have no empty boxes.
And finally your other question: the number of ways to distribute the 15 items if there are at least 2 empty boxes.
Let's consider different numbers of empty boxes.
Clearly there can't be 5 empty boxes.
(1) 4 empty boxes.
All 15 items must go in the one non-empty box; there is only 1 way to do that. And the non-empty box can be any one of the 5 boxes.
So with 4 empty boxes the number of ways of distributing the 15 items is 1*5 = 5.
(2) 3 empty boxes.
Now the 15 items must be distributed into the 2 non-empty boxes.
By stars and bars, the number of ways to do that is  .
And the number of ways of choosing the 3 empty boxes (or of choosing the 2 non-empty boxes) is "5 choose 2", which is 10.
So with 3 empty boxes the number of ways of distributing the 15 items is 16*10 = 160.
(3) 2 empty boxes.
Now the 15 items must be distributed into the 3 non-empty boxes.
By stars and bars, the number of ways to do that is  .
And the number of ways of choosing the 2 empty boxes (or of choosing the 3 non-empty boxes) is (again) "5 choose 2", which is 10.
So with 2 empty boxes the number of ways of distributing the 15 items is 136*10 = 1360.
ANSWER for your first question: with at least 2 empty boxes, the number of ways of distributing the 15 items is 5+160+1360 = 1525.
In the above analysis, the cases overlap, so the counts are faulty. The analysis below gives the correct results.
To check our results, we will determine the numbers of ways of distributing the 15 items with EXACTLY 0 empty boxes, or with EXACTLY 1 empty box, ..., or with EXACTLY 4 empty boxes. The sum of the numbers for the separate cases should be the total number of ways, which was determined earlier to be 3876.
The analysis for each case needs to do the following:
(1) determine the number of ways of choosing the given number of empty boxes from among the 5 boxes;
(2) put one item in each of the non-empty boxes to ensure that the number of empty boxes is correct for that case; and
(3) use stars and bars to determine the number of ways to distribute the remaining items in the non-empty boxes.
Exactly 0 empty boxes....
The number of ways of choosing 0 of the 5 boxes to be empty is "5 choose 0" = 1.
Put 1 item in each of the 5 non-empty boxes, leaving 10 items yet to be distributed.
Use stars and bars to find that the number of ways of distributing the remaining 10 items into 5 boxes is "14 choose 4": .
Number of ways with exactly 0 empty boxes: (1)(1001) = 1001.
Exactly 1 empty box....
The number of ways of choosing 1 of the 5 boxes to be empty is "5 choose 1" = 5.
Put 1 item in each of the 4 non-empty boxes, leaving 11 items yet to be distributed.
Use stars and bars to find that the number of ways of distributing the remaining 11 items into 4 boxes is "14 choose 3":  .
Number of ways with exactly 1 empty box: (5)(364) = 1820.
Exactly 2 empty boxes....
The number of ways of choosing 2 of the 5 boxes to be empty is "5 choose 2" = 10.
Put 1 item in each of the 3 non-empty boxes, leaving 12 items yet to be distributed.
Use stars and bars to find that the number of ways of distributing the remaining 12 items into 3 boxes is "14 choose 2":  .
Number of ways with exactly 2 empty boxes: (10)(91) = 910.
Exactly 3 empty boxes....
The number of ways of choosing 3 of the 5 boxes to be empty is "5 choose 3" = 10.
Put 1 item in each of the 2 non-empty boxes, leaving 13 items yet to be distributed.
Use stars and bars to find that the number of ways of distributing the remaining 13 items into 2 boxes is "14 choose 1":  .
Number of ways with exactly 3 empty boxes: (10)(14) = 140.
Exactly 4 empty boxes....
The number of ways of choosing 4 of the 5 boxes to be empty is "5 choose 4" = 5.
Put 1 item in the 1 non-empty box, leaving 14 items yet to be distributed.
Use stars and bars to find that the number of ways of distributing the remaining 14 items into 1 box is "14 choose 0" = 1.
Number of ways with exactly 4 empty boxes: (5)(1) = 5.
The total number of ways for the different numbers of empty boxes is
1001 + 1820 + 910 + 140 + 5 = 3876
This verifies that the numbers for the separate cases are correct.
So now we can answer your two questions correctly.
i) Number of ways of having at least two empty boxes: 910 + 140 + 5 = 1055
ii) Number of ways of having no empty box: 1001
Answer by ikleyn(52778)  (Show Source):
You can put this solution on YOUR website! .
How many ways are there to distribute 15  distinct items into 5 distinct boxes with:
i) At least two empty box.
ii) No empty box.
~~~~~~~~~~~~~~~~~~~~~
In this my post, I consider case (ii), ONLY.
The " stars and bars " method works for undistinguishable balls and distinguishable boxes, ONLY.
It is clear from the logic of this method. Many (if not all) autoritative sources point it directly.
See, for example, this Wikipedia article
https://en.wikipedia.org/wiki/Stars_and_bars_(combinatorics)
Therefore, it is inadequate and hopeless to apply the " stars and bars " method for the given problem,
where the balls are considered as DISTINGUISHABLE.
For it, another technique should be used. See my solution below.
The formula for the number of distributions of n distinguishable items in m distinguishable boxes is
F(n,m) =  . (1)
The sources for this formula are these references
Feller - An Introduction to Probability Theory and its Applications, Vol I, 3ed, 1968,
Chen Chuan-Chong, Koh Khee-Meng - Principles and Techniques in Combinatorics, 1992,
Anderson - A first course in combinatorial Mathematics, 2001.
To make calculations using this formula, I prepared Excel spreadshhets for some different values n and m.
Below are calculations for n= 3, m= 2 (three balls in two boxes).
k (-1)^k combin(2,k) (2-k)^3 Separate addends
of formula (1)
0 1 1 8 8
1 -1 2 1 -2
6 <<<---=== Final sum F(3,2)
You can check it manually that F(3,2) = 6 is the correct number of different distributions
of 3 distinguishable balls in 2 distinguishable boxes.
Below are calculations for n= 4, m= 2 (four balls in two boxes).
k (-1)^k combin(2,k) (2-k)^4 Separate addends
of formula (1)
0 1 1 16 16
1 -1 2 1 -2
14 <<<---=== Final sum F(4,2)
You can check it manually that F(4,2) = 14 is the correct number of different distributions
of 4 distinguishable balls in 2 distinguishable boxes.
Below are calculations for n= 15, m= 2 (fifteen balls in two boxes).
k (-1)^k combin(2,k) (2-k)^15 Separate addends
of formula (1)
0 1 1 32768 32768
1 -1 2 1 -2
32766 <<<---=== Final sum F(15,2)
It is not so easy to check it manually that F(15,2) = 32766 is the correct number of different distributions
of 15 distinguishable balls in 2 distinguishable boxes, but at least it seems likelihood.
And finally, below are calculations for n= 15, m= 5 (fifteen balls in five boxes, the requested case).
k (-1)^k combin(5,k) (5-k)^15 Separate addends
of formula (1)
0 1 1 30517578125 30517578125
1 -1 5 1073741824 -5368709120
2 1 10 14348907 143489070
3 -1 10 32768 -327680
4 1 5 1 5
25292030400 <<<---=== Final sum F(15,5)
ANSWER. The number of all different distributions of 15 distinguishable balls in 5 distinguishable boxes is 25292030400.
Solved.
//////////////////
Although the formula is given in the cited references, I think, there are not so many people who know
how to approach to the problem, who know about existing of this formula, who know on how to solve this problem in a right way.
This problem is of much higher level than average high school and even of much higher level than
an ordinary Math circle at a school or at a local University level.
Only professional mathematicians working in Combinatorial Math know about existing this formula.
Another circle of persons who can be competent in the area, are those who are professionally trained
to participate in International Math Olympiads, as well as their trainers and their teachers.
Third circle of such people are those who know well the relevant popular Math literature.
I myself do belong to this last category.
////////////////
Here one more tutor came (@rippletable) and brought an incorrect solution.
Ignore it, since it is incorrect.
Answer by rippletable(1)  (Show Source):
You can put this solution on YOUR website! For the first case consider taking away 2 boxes, then distributing the 15 distinct items into the 3 remaining distinct boxes.
There are 5 choose 2 ways to select the 2 boxes to take away. Then there are 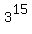 ways to distribute the items into the 3 remaining boxes, all in all you get:
|
|
|
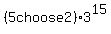
