Question 1196684: 1) There are 4 golden coins and 8 iron coins in a bag. You select one coin from the bag, if it is a golden coin, you keep it; but if it is an iron coin, you put it back in the bag. Find the probability of earning exactly 2 golden coins after:
a) Two consecutive selections
b) Three consecutive selections
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
************************************************************
**** NOTE ****
My solution to part (b) is different than that by tutor @ikleyn. Probably her answer is correct. I read part (b) to mean that exactly 2 gold coins are obtained in EXACTLY 3 selections -- but the statement of the problem doesn't say that.
So look at the solutions using both interpretations to see how they are different. They both show good mathematical methods; but they solve different problems.
************************************************************
Note that each time a gold coin is selected it is not returned to the bag, so the number of coins left in the bag decreases by 1; but when an iron coin is selected it is returned to the bag, so the number of coins remaining in the bag does not decrease.
(a) probability of 2 gold coins after 2 selections
Both selections must be gold.
P(gold,gold) = (4/12)(3/11) = 1/11
ANSWER: 1/11
(b) probability of 2 gold coins after exactly 3 selections
The third selection has to be gold; the first two can be either gold then iron or iron then gold.
P(gold,iron,gold) = (4/12)(8/11)(3/11) = 8/121
P(iron,gold,gold) = (8/12)(4/12)(3/11) = 2/33
The probability of 2 gold on exactly 3 selections is
8/121 + 2/33 = 24/363+22/363 = 46/363
ANSWER: 46/363
Answer by ikleyn(52940)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1) There are 4 golden coins and 8 iron coins in a bag. You select one coin from the bag,
if it is a golden coin, you keep it; but if it is an iron coin, you put it back in the bag.
Find the probability of earning exactly 2 golden coins after:
a) Two consecutive selections
b) Three consecutive selections
~~~~~~~~~~~~~~~~~~
I read, interpret and solve part (b) in other way (differently) than tutor @greenestamps.
Part (b)
There are 3 paths that lead to earning 2 golden coins after three selections:
(Golden, Golden, Iron); (Golden; Iron; Golden), and (Iron, Golden, Golden).
The partial/individual probabilities are
P(GGI) = 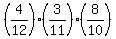 = = 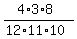 = 0.072727273 (rounded);
P(GIG) = = 0.072727273 (rounded);
P(GIG) = 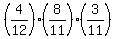 = = 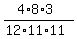 = 0.066115702 (rounded);
P(IGG) = = 0.066115702 (rounded);
P(IGG) = 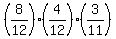 = = 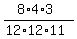 = 0.060606061 (rounded).
Next, I calculate the sum of the found partial probabilities and get the ANSWER:
P(to earn 2 golden coins after 3 selections) = 0.072727273 + 0.066115702 + 0.060606061 = 0.199449 (rounded). = 0.060606061 (rounded).
Next, I calculate the sum of the found partial probabilities and get the ANSWER:
P(to earn 2 golden coins after 3 selections) = 0.072727273 + 0.066115702 + 0.060606061 = 0.199449 (rounded).
Solved.
|
|
|