SOLUTION: There are 13 female board members and 17 male board members. How many ways are there to make a committee of 18 board members? How many ways are there to make a committee of 1

There are 13 + 17 = 30 board members, in all.


There are    different ways to select a committee of 18 board members.


Here    is the number of combinations of 30 persons taken 18 at a time.


The formula to calculate it is this


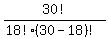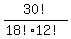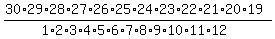     =  =  =  = 86493225.    ANSWER

A committee of 18 board members, which includes 7 females, should include  18-7 = 11 males.


7 females from 13 females ca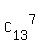n be chosen in   = 1716 different ways.

11 males  from 17   males can be chosen in 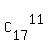  = 12376 different ways.


Combining these different teams, consisting of 11 males and 7 females, 

we have 1716*12376 = 21237216 different ways to make such a committee which is required in part (b).