Question 1193862: Three hunters each have a probability of 4/5 of hitting a target.
If each hunter fires exactly one shot at the target, what is the probability that it will be hit at least once?
I'm not sure if this is correct.
Two choices (hit or miss)
3 hunters
total outcomes 2^3 = 8
At least the target hit once,
so could be
- hit 1 time (3 take 1)= 3
- hit 2 times (3 take 2) =3
- hit 3 times (3 take 3) =1
p{(hit 1 time), (hit 2 times),(hit 3 times)}
3/8 + 3/8 + 1/8 = 7/8
then,
7/8 * 4/5 =28/40
= 7/10
Please help, thanks.
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
For this problem, the standard method of solution is as follows:
the probability that each separate shot will not hit the target is  = =  .
the probability that no one of the three shots will hit the target is .
the probability that no one of the three shots will hit the target is 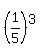 = = 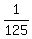 .
the probability that at least one shot will hit the target is the COMPLEMENT to .
the probability that at least one shot will hit the target is the COMPLEMENT to 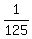 , i.e.
P = 1 - , i.e.
P = 1 - 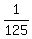 = =  . ANSWER . ANSWER
Solved.
MEMORIZE this chain of reasonings. It works in many other similar problems.
----------------
To get wider look, see the lesson
- Solving probability problems using complementary probability
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Solved problems on Probability".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
Consider these lessons as your textbook, handbook, a Solutions Manual, tutorials and (free of charge) home teacher.
Happy learning ( ! )
/////////////
Responding to the question in your comment:
Another way to solve the problem is to use the formula
P(at least one hits) = p(hmm) + p(mhm) + p(mmh) + p(hhm) + p(hmh) + p(mhh) + p(hhh)
= 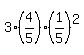 + + 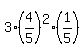 + +  ,
where "h" means "hits", "m" means "misses".
But it requires much more calculations and, THEREFORE, is not a front line formula/method. ,
where "h" means "hits", "m" means "misses".
But it requires much more calculations and, THEREFORE, is not a front line formula/method.
|
|
|