Question 1192625: How many different 4-letter permutations can be formed from the letters in the word WESTINGHOUSE?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(53299)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many different 4-letter permutations can be formed from the letters in the word WESTINGHOUSE?
~~~~~~~~~~~~~~~~~~~~~~
It is clear that the correct question is to find the number of all distinguishable 4-letter arrangements
(not permutations).
So, I will solve the problem in this  formulation. formulation.
The given word consists of 12 letters.
Of them, 8 letters are non-repeating; two letters (E and S) are repeating and have multiplicity 2.
So, I first consider 10 unique letters W, E, S, T, I, N, G, H, O, U and will calculate the number of 4-letter
arrangements of these letters. All these arrangements consist of non-repeating letters.
Then I will consider all 4-letter distinguishable words having two repeating "E" and no repeating "S";
then I will consider all 4-letter distinguishable words having two repeating "S" and no repeating "E";
then I will consider all 4-letter distinguishable words having two repeating "E" and two repeating "S".
At the end, I will add all these opportunities.
(1) the number of 4-letter arrangements of 10 distinct letters W, E, S, T, I, N, G, H, O, U is
10*9*8*7 = 5040.
(2) the number of all 4-letter distinguishable words having two repeating "E" is
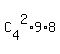 = = 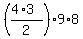 = 6*9*8 = 432.
Here = 6*9*8 = 432.
Here 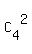 = = 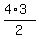 = 6 is the number ow ways to select two positions for E in the 4-letter word,
without looking the order. Next, the factors 9 and 8 are to calculate the number of placing the rest unique letters
at the remaining two positions in the 4-letter word.
(3) the number of all 4-letter distinguishable words having two repeating "S" is = 6 is the number ow ways to select two positions for E in the 4-letter word,
without looking the order. Next, the factors 9 and 8 are to calculate the number of placing the rest unique letters
at the remaining two positions in the 4-letter word.
(3) the number of all 4-letter distinguishable words having two repeating "S" is
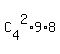 = = 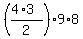 = 6*9*8 = 432.
Here = 6*9*8 = 432.
Here 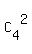 = = 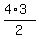 = 6 is the number ow ways to select two positions for S in the 4-letter word,
without looking the order. Next, the factors 9 and 8 are to calculate the number of placing the rest unique letters
at the remaining two positions in the 4-letter word.
(4) the number of 4-letter distinguishable words having two repeating "E" and two repeating "S" is = 6 is the number ow ways to select two positions for S in the 4-letter word,
without looking the order. Next, the factors 9 and 8 are to calculate the number of placing the rest unique letters
at the remaining two positions in the 4-letter word.
(4) the number of 4-letter distinguishable words having two repeating "E" and two repeating "S" is
 = =  = 6.
Finally, I sum up the found numbers 5040 + 432 + 432 + 6 = 5910.
ANSWER. There are 5910 such distinguishable 4-letter words. = 6.
Finally, I sum up the found numbers 5040 + 432 + 432 + 6 = 5910.
ANSWER. There are 5910 such distinguishable 4-letter words.
Solved.
Answer by math_tutor2020(3827)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We'll need to break things into multiple cases.
Here's the table of contents
Case A) All four letters are unique
Case B) We have two copies of "E" and everything else is unique.
Case C) We have two copies of "S" and everything else is unique.
Case D) We have two copies of "E" and two copies of "S"
---------------------------------------------------------------
Case A) All four letters are unique
Example word could be: WEST
In the word "WESTINGHOUSE", the unique letters in the order presented are:
{W, E, S, T, I, N, G, H, O, U}
There are 10 letters in this list.
Notice that I didn't write the second copy of "S" nor the second copy of "E".
If it might help, then we can write the list of letters out like this
{W, E, S, T, I, N, G, H, O, U, S, E}
but cross out the last two letters since they were mentioned earlier
{W, E, S, T, I, N, G, H, O, U, S, E}
so that's how I got to
{W, E, S, T, I, N, G, H, O, U}
Since we have n = 10 unique letters to work with, and r = 4 slots to fill, this means we can use the nPr permutation formula. Order matters.
n P r = (n!)/( (n-r)! )
10 P 4 = (10!)/( (10-4)! )
10 P 4 = (10!)/(6!)
10 P 4 = (10*9*8*7*6!)/(6!)
10 P 4 = 10*9*8*7
10 P 4 = 5040
Or perhaps more intuitively, we start off with 10 and count down by 1 each time until we have four slots to fill. So that helps explain why 10*9*8*7 is buried in the nPr formula when n = 10 and r = 4.
There are 5040 ways to select four letters such that all of them are unique.
Let A = 5040 so we can use it later.
---------------------------------------------------------------
Case B) We have two copies of "E" and everything else is unique.
Example "word" could be: WESE
Let's say we label the slots 1,2,3,4.
There are 4 choices to place "E", and then there are 3 choices left to place the other E. That gives 4*3 = 12, but we divide by 2 since we cannot tell the "E"s apart. That leads us to 12/2 = 6 ways to place the "E"s.
Put another way, there are 4 C 2 = 6 ways to place those two "E"s. I'm using the nCr combination formula.
Go back to
{W, E, S, T, I, N, G, H, O, U, S, E}
and cross off the duplicate "S" and both copies of "E"
{W, E, S, T, I, N, G, H, O, U, S, E}
we're left with
{W, S, T, I, N, G, H, O, U}
which has n = 9 letters in it.
After placing those "E"s, there are r = 2 slots left to fill.
Meaning we have nPr = 9 P 2 = 9*8 = 72 ways to fill the remaining two slots.
We found there are 6 ways to place the "E"s and 72 ways to select the remaining other unique letters.
There are 6*72 = 432 ways to carry out case B.
Let B = 432 so we can use it later.
---------------------------------------------------------------
Case C) We have two copies of "S" and everything else is unique.
Example "word" could be: WSSE
The steps are identical to case B.
This is because "S" repeats just as much as "E" does.
This means there are 432 ways to place the two "S" letters, and fill in the remaining slots with other unique letters.
Let C = 432
---------------------------------------------------------------
Case D) We have two copies of "E" and two copies of "S"
Example word: SEES
There are 6 ways to place the "E"s in whatever two slots they land in. Refer to the 4 C 2 = 6 mentioned earlier in case B. The two "S" letters will have no choice but to fill the remaining empty slots in exactly one way.
The order of which you pick doesn't matter, so you could start with the "S" letters first, then move onto the "E"s later.
In short, there are 6 ways to carry out case D.
Let D = 6.
---------------------------------------------------------------
To wrap everything up, we'll add up the results of each case mentioned earlier.
Such addition is possible because cases A,B,C,D are mutually exclusive.
Only one case can happen at a time and there is no overlap.
A+B+C+D = 5040+432+432+6 = 5910
This can be verified by using computer software to generate all the possible permutations.
This is a really awesome free calculator that will do just that
https://www.mathsisfun.com/combinatorics/combinations-permutations-calculator.html
It not only lists the numeric nCr and nPr values, but it will also list all the actual sequences possible.
Though I imagine there's a size limit so it cannot list every possible set.
Luckily, our set isn't too large.
Type these letters
W, E, S, T, I, N, G, H, O, U, S, E
into the box where it mentions "List Them:"
Don't input any curly braces or quotation marks. Each letter must be separated by a comma.
Make sure to change the "Types to choose from?" to 12 and "Number Chosen?" to 4.
Set "is order important" to "yes", and set "repetition allowed?" to "no".
Otherwise, the solver will likely list the wrong thing you're after.
Check out the screenshot to see what I mean.

Click on the "list" button at the bottom to have the solver mention 5910 different four letter permutations after tossing the duplicates.
Before tossing the duplicates, there are 12 P 4 = 12*11*10*9 = 11,880 entries.
---------------------------------------------------------------
Answer: 5910
|
|
|