Question 1191631: How many distinct permutations of 4 letters from EAGLES are there?
I first tried to do cases.
My first case was to leave out all the non-repeated letters so I ended up with 4•4!/(2!) = 48
My second case was to leave out all repeated letters and ended up with 1•4!/(1!) = 24
When I add them, it equals up to uw permutations but my answer key says 192 permutations. Please help me find where I went wrong with this question! Thanks!
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The word EAGLES has 6 letters; of them, one letter E is repeated and have a multiplicity 2.
When we analyze the number of different words of 4 letters formed from the given word (symbols),
we should distinct two different cases.
Case 1. All 4 letters in the final word are different.
In this case, we have only 5 distinct letters to choose from, (E, A, G, L S);
therefore, the number of possible words to form is 5*4*3*2 = 120 in this case (the order of letters does matter !);
Case 2. In the final word, we have 2 identical letters E and any 2 of the remaining 4 letters.
In this case, we can select these two remaining letters by 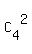 = 6 different ways,
and we can arrange then 4 letters with two repeating undistinguishable Es by = 6 different ways,
and we can arrange then 4 letters with two repeating undistinguishable Es by
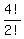 = =  = 12 different distinguishable ways.
Combining everything altogether, we have 6*12 = 72 different words in Case 2.
Cases (1) and (2) are the disjoint sets of words; therefore, the answer to the problem's question is 120 + 72 = 192.
ANSWER. 192 different / (distinguished) words of the length 4 can be formed. = 12 different distinguishable ways.
Combining everything altogether, we have 6*12 = 72 different words in Case 2.
Cases (1) and (2) are the disjoint sets of words; therefore, the answer to the problem's question is 120 + 72 = 192.
ANSWER. 192 different / (distinguished) words of the length 4 can be formed.
Solved.
|
|
|