Question 1189702: The letters C,I,R,C,L, and E can be used to form 6-letter strings such as CIRCLE or CCIRLE. Using these letters, how many different 6-letter strings can be formed in which the two occurrences of the letter C are separated by at least one other letter?
a)96 b)120 c)144 d)180 e)240
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website! .
The letters C,I,R,C,L, and E can be used to form 6-letter strings such as CIRCLE or CCIRLE.
Using these letters, how many different 6-letter strings can be formed in which the two occurrences
of the letter C are separated by at least one other letter?
a)96 b)120 c)144 d)180 e)240
~~~~~~~~~~~~~~~
(1) From the context, it is clear that they want you consider only DISTINGUISHABLE strings.
(2) In the word "CIRCLE", there are 6 letters; of them, letter C is of multiplicity 2.
THEREFORE, the number of all possible distinguishable strings is 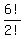 = 720/2 = 360.
(3) Of them, the number of all distinguishable strings with two attached (glued) letters C is (6-1)! = 5! = 120.
These 120 strings are UNFAVORABLE. The rest 360-120 = 240 distinguishable strings are favorable.
ANSWER. There are 240 distinguishable strings, where two occurrences of the letter C are separated by at least one other letter.
Option e)
Solved and explained.
|
|
|
