Question 1189667: (1)
(2) How many different ways can 3 red, 4 yellow and 2 blue bulbs be arranged in a string of Christmas tree lights with 9 sockets?
(3)
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
(1)
(2) How many different ways can 3 red, 4 yellow and 2 blue bulbs be arranged in a string of Christmas tree lights with 9 sockets?
(3)
~~~~~~~~~~~~~~~
Of the three different problems posted, I will solve the second one, ONLY.
The total number of sockets is 9.
There are 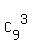 = =  = 84 different ways to select 3 sockets from 9 sockets for 3 red bulbs.
There are = 84 different ways to select 3 sockets from 9 sockets for 3 red bulbs.
There are 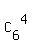 = = 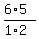 = 15 different ways to select 4 sockets from 9-3 = 6 remaining sockets for 4 yellow bulbs.
After that, the sockets for remaining 2 blue bulbs are the remaining 2 sockets, so there is only 1 way to place them (there is no other choice).
In all, there are 84*15 = 1260 ways to arrange the bulbs, according to the Fundamental counting principle. ANSWER = 15 different ways to select 4 sockets from 9-3 = 6 remaining sockets for 4 yellow bulbs.
After that, the sockets for remaining 2 blue bulbs are the remaining 2 sockets, so there is only 1 way to place them (there is no other choice).
In all, there are 84*15 = 1260 ways to arrange the bulbs, according to the Fundamental counting principle. ANSWER
There is another method to solve the problem.
Among 9 bulbs, we have 3 indistinguishable red bulbs; 4 indistinguishable yellow bulbs and 2 indistinguishable blue bulbs.
So, we apply the formula for distinguishable/indistinguishable permutations and find the number of distinguishable arrangements
 = 1260,
which gives the same answer. = 1260,
which gives the same answer.
Solved by two different methods, giving the same answer.
------------------
To learn the subject, see my lessons
- Introduction to Combinations
- PROOF of the formula on the number of Combinations
- Problems on Combinations
- Fundamental counting principle problems
- Arranging elements of sets containing indistinguishable elements
in this site. Find there many other similar and different solved problems.
////////////
Here I explain, why I solved only one problem and ignored two others.
It is because the rules of this forum PROHIBIT posting more than one problem per post.
Why it is so ? - - - BECAUSE this forum's task and profile is to TEACH.
When a person/(a visitor) posts more than one problem per post,
it means only one thing : his or her goal is everything except of learning.
About the rules and the policy of this forum read at this web-page
https://www.algebra.com/tutors/students/ask.mpl?action=ask_question&topic=Equations&return_url=http://www.algebra.com/algebra/homework/equations/
from which you post your problems.
It is assumed that you read these rules before posting.
It is also assumed that you do understand what is written in that page and follow the rules.
Those who violate them, work against their own interests.
*******************************************************************
So P L E A S E post your problems S E P A R A T E L Y (!)
*******************************************************************
|
|
|