Question 1189564: Find how many different groups of 2 elements, with repetition, can be formed
with the letters: a, b, c, d. I solved it like this: 5!/2!*2!=10, but im not sure
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
Find how many different groups of 2 elements, with repetition, can be formed
with the letters: a, b, c, d.
I solved it like this: 5!/2!*2!=10, but im not sure
~~~~~~~~~~~~~~~
Your solution is INCORRECT. (Notice that the number of 5 is irrelevant to the problem,
so 5! is nowhere to come . . . )
The answer and the solution depend on one important agreement: if you consider ORDERED or UNORDERED pairs.
Unfortunately, your problem does not specify, if the pairs are ordered or unordered, and it is the problem's FAULT.
=============== S O L U T I O N ===============
for ORDERED pairs
From the context, there are many/enough instances of each letter (more concretely, at least two instances of each letter).
You have 4 letters.
If repetition is allowed, then you may have any of 4 letters in the first position and any of 4 letters in the second position.
In all, it gives 4*4 = 16 different groups of 2 letters each.
For UNORDERED pairs
For unordered pairs, the pair (a,b) is the same as (b,a).
Then there are 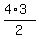 = 6 pairs with different (non-repeating) letters
PLUS 4 pairs with repeating letters (a,a), (b,b), (c,c) and (d,d).
It gives, in total, 6 + 4 = 10 such groups.
So, there are two agreements; two way to form pairs, and, correspondingly, there are two different answers.
Again : the fact that the problem does not specify which of the two possible agreements work - - - is the FAULT of the problem.
-------------
Visually, the model for the first case is a full 4 x 4 matrix filled with ordered pairs of letters (16 ordered pairs).
For the second case, the model is the upper triangular part of the 4 x 4 matrix with its diagonal included.
|
|
|
