SOLUTION: How many 9-digit codes can be formed if the code starts with 000 or ends with 1?

To solve the problem, we should calculate separately

    - the number of the 9-digit codes that start with 000;

    - the number of the 9-digit codes that end with 1;

    - and then calculate the number of the codes in the union of these two sub-sets.


(1)  The number of the 9-digit codes that start with 000 is  = ,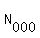

     since the first three digits are just pre-determined, and only 6 remaining positions 
     each may have any of 10 digits.


(2)  The number of the 9-digit codes that end with  is  = ,

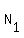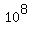     since the last digit is just pre-determined, and only 8 remaining positions 
     each may have any of 10 digits.


(3)  To complete the solution, apply the formula for the union

          =  +  - .


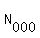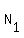       equals to 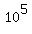 , since the intersection is the set of all codes

     that have pre-determined 000 in the first 3 positions and 1 in the last position,
     having all 5 = 9-3-1 positions free for any of 10 digits.


     THEREFORE, the final formula and the final answer are

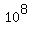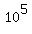          =  +  -  = 1,000,000 + 100,000,000 - 100,000 = 100,900,000.


ANSWER.  There are  100,900,000  such codes.