Question 1187221: If C(n,4)=C(n,10). What is the value of n?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i think it's 14.
c(14,4) = 1001
c(14,10) = 1001
the value of n would be equal to 4 + 10 = 14.
the formula for c(n,x) = n! / (x! * (n-x)!)
when x = 4, the formula becomes c(n,4) = n! / (4! * (n-4)!).
when x = 10, the formula becomes c(n,10) = n! / (10! * (n-10!)).
when c(n,4) = c(n,10), the formula becomes n! / (4! * (n-4)!) = n! / (10! * (n-10)!).
since n! is in both equations, then, for these to be equal, 4! * (n-4)! must be equal to 10! * (n-10)!.
these would be equal if (n-4)! = 10! and (n-10)! = 4!.
you would then get 4! * 10! = 10! * 4!.
for (n-4)! to be equal to 10!, n-4 must be equal to 10, and for (n-10)! to be equal to 4!, n - 10 must be equal to 4.
if n - 4 = 10, then n must be equal to 14.
if n - 10 = 4, then n must be equal to 14.
it looks like n has to be equal to 14.
note that 10 + 4 = 14.
assuming n = 14, you get:
c(14,4) = 14! / (4! * 10!) and you get c(14,10) = 14! / (10! * 4!).
when you work them through, you get:
14! / (4! * 10!) = 1001
14! / (10! * 4!) = the same.
your solution is that the value of n = 14.
here is the complete set of combination formulas for c(n,x) where n = 14 and x equal 0 to 14.
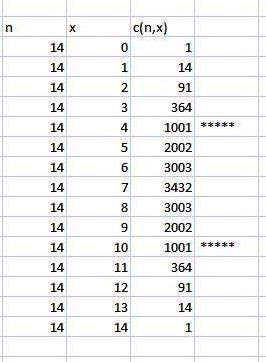
as you can see, there is some symmetry in the values.
c(n,x) is equal to c(n,(n-x)).
when n = 14 and x = 4, you get:
c(14,4) is equal to c(14,10).
another example:
c(14,3) = 364
c(14,14-3) = c(14,11) = 364.
|
|
|