SOLUTION: How many ways can the letters of the word MISSISSIPPI be arranged if no two S's are side by side?

Algebra ->  Permutations -> SOLUTION: How many ways can the letters of the word MISSISSIPPI be arranged if no two S's are side by side?      Log On


   

Question 1183742: How many ways can the letters of the word MISSISSIPPI be arranged if no two S's are side by side?
Answer by ikleyn(52780) About Me  (Show Source):
You can put this solution on YOUR website!
.
How many ways can the letters of the word MISSISSIPPI be arranged if no two S's are side by side?
~~~~~~~~~~~~~~~~~~~~~


Since you use the term "arranged", I will assume that you know the difference between permutations and arrangements,
and between distinguishable and undistinguishable arrangements/permutations. 


First, take off all letters S from the word. You will get

      MIIIPPI


Next, insert blanks between the remaining letters.  Also, place blanks before the first letter and after last letter.

You will get


    _M_I_I_I_P_P_I_


with 8 blanks.  


Now you have 7-letters word MIIIPPI with 4 repeating letter I  and 2 repeating letters P.

You can arrange them in 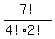 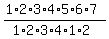7%21%2F%284%21%2A2%21%29 = %281%2A2%2A3%2A4%2A5%2A6%2A7%29%2F%281%2A2%2A3%2A4%2A1%2A2%29 = 105 distinguishable ways.    (1)



Finally, you distribute four letters S, one after one, among 8 blank positions, placing one S into one blank.

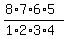You can do it by  C%5B8%5D%5E4 = %288%2A7%2A6%2A5%29%2F%281%2A2%2A3%2A4%29 = 70 ways.    (2)



Now, combining 105 arrangements (1) with 70 independent arrangements (2), you have 105*70 = 7350 total possible arrangements 
of the word MISSISSIPPI with no two S's side by side.

Solved.