Question 1182155: Hello, I found this question in the permutations and combinations chapter of my math's textbook. I need help to understand and solve it.
Find the probability of obtaining exactly:
(a) 3 heads from 5 tosses of a coin
textbook answer says its 5/16, but shouldn't the answer be 3/10? (3 the event and 10 all possibilities including heads and tails)
There are more questions like these like:
(b) 2 heads from 8 tosses of a coin
(c) 6 heads from 8 tosses of a coin
(d) 2 heads from 4 tosses of a coin
(e) 10 heads from 20 tosses of a coin
answers for these are:
(b)7/64
(c)7/64
(d)3/8
(e) 184756/1048576
Found 2 solutions by math_tutor2020, greenestamps:
Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!
Part (a)
Let's label the five slots as A,B,C,D,E.
Each slot has the option of heads (H) or tails (T)
One such configuration could be HHHTT.
We could also have HHTHT
Each case involves three H's and two T's.
The question is: how many ways can we rearrange those sequences of H's and T's?
Let's rephrase the problem a slightly different way. Let's say we have 5 slips of paper, and each paper has a single letter A through E on it.
If we randomly picked out slips of paper, then we might get this sequence:
AEB,CD
The first three letters would tell us which slots get H and the remaining two letters get T
So that sequence would then tell us we got HHTTH
-----------------------------
So we need to find the number of ways to select three letters from A,B,C,D,E. The order doesn't matter.
That's a combination problem involving the nCr formula. We plug in n = 5 and r = 3. You should get 10 different ways.
Another approach you could take is to realize that there are 5*4*3 = 60 different permutations possible and 60/(3!) = 60/(3*2*1) = 60/6 = 10 combinations.
-----------------------------
We found there are 10 ways to get exactly three heads where the order doesn't matter.
This is out of 2^5 = 32 ways to flip five coins.
Therefore,
10/32 = (2*5)/(2*16) = 5/16 is the final answer for part (a).
====================================================
Part (b)
This part is basically the same as part (a), but the numbers are different of course.
We have n = 8 coins and we want r = 2 heads. I'll use the nCr combination formula to show a different approach.
nCr = (n!)/(r!*(n-r)!)
8C2 = (8!)/(2!*(8-2)!)
8C2 = (8*7*6!)/(2!*6!)
8C2 = (8*7)/(2!) ...... a pair of 6! terms cancel
8C2 = (8*7)/(2*1)
8C2 = 56/2
8C2 = 28
We have 28 ways to get exactly 2 heads. The number 28 is found in Pascal's triangle in the row that reads 1,8,28,...
There are 2^n = 2^8 = 256 ways to flip 8 coins
The probability we want is 28/256 = (4*7)/(4*64) = 7/64 which is the final answer.
====================================================
Part (c)
I'll use yet another approach. I mentioned Pascal's triangle earlier so why not go over an example of it.
Look at the row that has 1,8,28... in it. At the very end of the row, you should notice the same exact pattern except that it's backwards.
Start at the very far right end (1). That corresponds to slot 8. Move one spot to the left and you'll get to 8, which is for slot 7. Slot 6 will get us to 28.
This means that nCr = 8C6 = 28. The triangle has nice symmetry we can quickly determine combination values from.
Why does this work? Well the idea of getting 6 heads is basically the same as getting 2 tails. If we want to know how many exact ways to getting 2 tails, then we just follow the steps done in part (b) earlier and we should get 28 ways. The labels "heads" and "tails" don't really matter since either side is equally likely. We can easily flip the labels and get the same thing.
So that's why 7/64 is the answer here, and it's not a coincidence that parts (b) and (c) have the exact same answer.
====================================================
Part (d)
You should find that there are...
nCr = 4C2 = 6 ways to get exactly two heads
2^n = 2^4 = 16 ways to flip four coins.
Therefore, 6/16 = (2*3)/(2*8) = 3/8 is the probability we want.
====================================================
Part (e)
Same story as before, but different numbers
nCr = 20C10 = 184,756 ways to get ten heads
2^n = 2^20 = 1,048,576 ways to flip twenty coins
We end up with the fraction (184,756)/(1,048,576)
aka 184756/1048576
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
There are 2 possible outcomes on each toss of the coin. The total number of possible outcomes is 2*2*2*2*2=32. It looks as if you did 2+2+2+2+2=10.
Make sure you understand why you multiply the 2's instead of adding them. It's the fundamental counting principle: if there are m ways to do one thing and n ways to do another thing (and those two things are independent), then the number of ways to do those two things one after the other (or at the same time) is m times n.
In this problem, you are doing 5 things (the 5 coin tosses), each of which has 2 possible outcomes, so you multiply all those 2's together to get the total number of possible outcomes.
There are not only 3 ways to get 3 heads in 5 tosses. The number of ways of getting 3 heads in 5 tosses is "5 choose 3", often denoted by either C(5,3) or 5C3 (we need to choose 3 of the 5 tosses to be heads). Mathematically, the computation for 5C3 is
So the probability for this first problem is 10/32 = 5/16.
The other problems are worked in exactly the same way:
n tosses means 2^n possible outcomes
m heads (or tails) in n tosses can happen in nCm ways
The probability of m heads (or tails) in n tosses is 
A couple of things to keep in mind when you are calculating nCm values:
(1) As an example, 10C7 is the same as 10C3.
10C3 means you are choosing 3 of the 10 items; that means you are choosing NOT to choose 7 of the 10 items. So 10C7 is the same number as 10C3.
(2) After you have performed the nCm calculation a few times for different problems, stop going clear back to the definition of nCm. Here is an example:
To calculate 10C7, first change that to 10C3, since those are the same number.
Then the computation for 10C3 is a fraction with 3 factors in both numerator and denominator; the numbers in the numerator start with 10 and count down, and the numbers in the denominator start with 3 and count down:
I'll show the calculation for one more of your problems as a further example.
(d) 2 heads in 4 tosses
The number of possible outcomes is 2^4=16
The number of ways of getting 2 heads in 4 tosses is 
The probability is 6/16 = 3/8
I leave (b) to you; you know what the answer is supposed to be, so you can check your work.
Note that the answer for (c) is going to be the same as the answer to (b) -- because in (b) the numerator of the probability fraction is 8C2 and in (c) the numerator is 8C6. But (from the first note above) 8C6 and 8C2 are the same number.
For (e) the probability is going to be 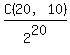 . Those are not calculations you want to do by hand; and you can see the answer is "ugly". Find a calculator to verify the given answer for that problem.
Or, if you now feel comfortable with the process for finding the answers for problems like this, simply skip the last example. (Working with the big ugly numbers won't teach you anything more about the PROCESS for finding the answer).
|
|
|
