Question 1177886: In how many ways can you place 4 red balls,3 yellow balls,6 black balls,2 blue balls,and 1 orange ball in a row?
Found 2 solutions by ikleyn, math_helper:
Answer by ikleyn(52777)   (Show Source):
You can put this solution on YOUR website! .
In 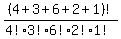 =  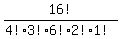different ways.
Complete calculations on your own.
Solved, instructed.
------------------
To see other similar solved problems, look into the lesson
- Arranging elements of sets containing indistinguishable elements
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Combinatorics: Combinations and permutations".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
Answer by math_helper(2461)  (Show Source):
You can put this solution on YOUR website!
This is analogous to the number of distinguishable arrangements of the 16 letters {A,A,A,A,B,B,B,C,C,C,C,C,C,D,D,E}
16!/(4!*3!*6!*2!*1!) = 100900800 ways.
|
|
|
