Question 1177055: 1. A and B play 12 games of chess of which 6 are won by A,4 are won by B and two ends in a tie. They agree to play a tournament consisting of 3 games. Find the probability that
a) A wins all three games
b) Two games end in a tie
c) A and B wins alternatively
d) B wins at least one game
Found 2 solutions by ewatrrr, ikleyn:
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi
12games: A wins 6, B wins 4, 2 T
Play 3 games:
a) P(A wins all three games) = (1/2)(1/2)(1/2) = 1/8
b) P(Two games end in a tie) = (3C2)(5/6)(1/6)(1/6) = 15/216
c) P(A and B wins alternatively) =
P(ABA) + P(BAB) = (1/2)(1/3)(1/2) + (1/3)(1/2)(1/3) = 1/12 + 1/18 = 30/12*18 = 5/36
d) P( B wins at least one game) = 1 - P(wins NO games) = 1- 1/8 = 7/8
Wish You the Best in your Studies.
Answer by ikleyn(52932)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A and B play 12 games of chess of which 6 are won by A, 4 are won by B and two ends in a tie.
They agree to play a tournament consisting of 3 games. Find the probability that
a) A wins all three games
b) Two games end in a tie
c) A and B wins alternatively
d) B wins at least one game
~~~~~~~~~~~~~~~
This problem is, actually, a standard problem of this class, but expressed in slightly unusual terms,
which may create difficulties to you in understanding its meaning.
Therefore, I will re-formulate this problem EQUIVALENTLY in familiar terms.
+------------------------------------------------------------------------+
| In a bag, there are 6 black balls (A wins), 4 white balls (B wins) |
| and 2 blue balls (ends in a tie). |
| You draw 3 of these balls randomly without replacement. |
| (a) What is the probability to draw 3 black balls ? |
| (b) Two balls are blue |
| (c) White and Black ball are drawn alternatively |
| (d) B wins at least one game |
+------------------------------------------------------------------------+
So I will solve this problem with the balls, instead of considering chess games played in a tournament.
SOLUTION
(a) In all, there are 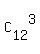 = = 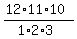 = 220 different triples of balls.
It is the samples space.
Of them, there are = 220 different triples of balls.
It is the samples space.
Of them, there are 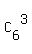 = = 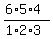 = 20 triples consisting of black balls
(analog to "A wins all three games").
THEREFORE, the probability under the problem's question is = 20 triples consisting of black balls
(analog to "A wins all three games").
THEREFORE, the probability under the problem's question is 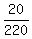 = =  . ANSWER
(b) In this case, there are . ANSWER
(b) In this case, there are 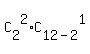 = 2*10 = 20 favorable cases.
THEREFORE, the probability under the problem's question is = 2*10 = 20 favorable cases.
THEREFORE, the probability under the problem's question is 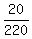 = =  . ANSWER
(c) In this case. P = P(White,Black,White) + P(Black,White,Black) = . ANSWER
(c) In this case. P = P(White,Black,White) + P(Black,White,Black) =
 + + 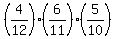 = = 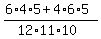 = = 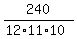 = = 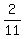 . ANSWER . ANSWER
Solved.
///////////
At this point, I will stop.
I left part (d) unsolved - because I don't like to have (to solve) toooooooo many problems in one post.
PLEASE DO NOT PACK many / (tooooo many) problems in one post.
It is PROHIBITED by the rules of this forum, and it ALWAYS works against your own interests.
-------------
The solution by @ewatrrr is INCORRECT, and her interpretation of the problem is INCORRECT, too.
So, ignore her post for your safety.
|
|
|