Question 1175410: A caterer is arranging a row of desserts. The row will contain 8 platters of cookies, 5 trays of fruit, and 3 pies. In how many distinct ways can the cookies, fruit, and pies, be arranged in a row, if each type of desert is of the same kind?
Found 2 solutions by ewatrrr, ikleyn:
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi
16 desserts: 13 cookies and fruit offerings (not exactly the same),
3 pies identical.
(Similar to distinct ways of arranging letters in a word when 3 of the letters are the same)
distinct ways of arranging in a row: 16!/3!
Wish You the Best in your Studies.
Answer by ikleyn(53538)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
As I understand/interpret this problem, there are 8 + 5 + 3 = 16 items, in all.
Of them, 8 platters are identical (indistinguishable; cookies, letter C);
5 other platters are identical (indistinguishable; fruits, letter F);
3 other platters are identical (indistinguishable; pies, letter P).
The question is, how many distinguishable arrangements of these letters/items
of the length 16 can be made ?
Same as to ask how many distinguishable words of the length 16 can be arranged having 8 identical letters C;
5 identical letters F and 3 identical letters P.
The answer is 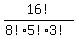 = = 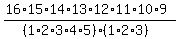 = 720720. = 720720.
Solved.
There is NOTHING IN COMMON with the solution by @ewatrrr.
----------------
To see other similar solved problems, look into the lesson
- Arranging elements of sets containing indistinguishable elements
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Combinatorics: Combinations and permutations".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|