Question 1175303: How many 12-bit strings (that is, bit strings of length 12) are there which:
have weight 7 and either start with 011 or end with 01 (or both)?
There were three questions before this which I have worked the answers to, but I'm confused for this part.
Other questions:
a. Q. Start with the sub-string 001? A. 2^9
b. Q. Have weight 7 (i.e., contain exactly 7 1's) and start with the sub-string 001? A. C(9,5)
c. Q. Either start with 011 or end with 01 (or both)? A. 2^9 + 2^10 - 2^7
Answer by ikleyn(52943)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many 12-bit strings (that is, bit strings of length 12) are there which:
have weight 7 and either start with 011 or end with 01 (or both)?
There were three questions before this which I have worked the answers to, but I'm confused for this part.
Other questions:
a. Q. Start with the sub-string 001? A. 2^9
b. Q. Have weight 7 (i.e., contain exactly 7 1's) and start with the sub-string 001? A. C(9,5)
c. Q. Either start with 011 or end with 01 (or both)? A. 2^9 + 2^10 - 2^7
~~~~~~~~~~~~~~~~
Let me rewrite the problem (the first two lines) in a way understandable for ANYONE.
The word of 12 symbols is written using symbols "1" and "0".
How many such words do exist, having 7 symbols "1" and
(a) starting from "011" ?
(b) ending with "01" ?
(c) starting from "011" and ending with "01".
Questions (a), (b) and (c) are three SEPARATE questions.
Now everything is clear. See my solution below.
Solution
(a) Three leftmost positions are just occupied and, THEREFORE, are not the subject of consideration.
For the rest 12-3 = 9 positions, we have 7-2 = 5 "ones" to distribute.
We can choose these 5 positions for "ones" from 9 positions by 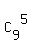 ways.
(b) Two rightmost positions are just occupied and, THEREFORE, are not the subject of consideration.
For the rest 12-2 = 10 positions, we have 7-1 = 6 "ones" to distribute.
We can choose these 6 positions for "ones" from 10 positions by ways.
(b) Two rightmost positions are just occupied and, THEREFORE, are not the subject of consideration.
For the rest 12-2 = 10 positions, we have 7-1 = 6 "ones" to distribute.
We can choose these 6 positions for "ones" from 10 positions by  = =  ways.
(c) Three leftmost positions and two rightmost positions are just occupied and, THEREFORE, are not the subject of consideration.
For the rest 12-3-2 = 7 positions, we have 7-2-1 = 4 "ones" to distribute.
We can choose these 4 positions for "ones" from 7 positions by ways.
(c) Three leftmost positions and two rightmost positions are just occupied and, THEREFORE, are not the subject of consideration.
For the rest 12-3-2 = 7 positions, we have 7-2-1 = 4 "ones" to distribute.
We can choose these 4 positions for "ones" from 7 positions by 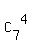 ways. ways.
Solved. All questions (a), (b) and (c) are answered.
Is everything clear to you from my post ?
If you still have questions, then let me know.
/\/\/\/\/\/\/\/
It is how a Math problem should be presented and solved.
Crystally clear for EVERYONE.
How it was worded and presented in your original post, is good for recycling, only.
Probably (I am ready to admit it) it is not your fault, but then it is the fault of the person, who composed this problem . . .
Also, for the future, if you have several questions, it is ALWAYS better to separate them and to submit them ONE per POST.
|
|
|