SOLUTION: Please help me to solve this Qeustion(1) Prove that nCr=n+1Cr-nCr-1 and Qeustion (2) Prove that nPr=(n-r+1) *nPr-1

1) nCr = n!/((n-r)!r!)   <<< this is what we need to show for the RHS



  RHS: C(n+1,r) - C(n,r-1)   where C(a,b) = "aCb"

   

 = 



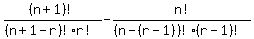
Factor out n+1 from the first term, and multiply the 2nd term by r/r:

 = 



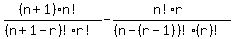
Notice (n+1-r)! ( = (n-(r-1))! ) is the same as  (n+1-r)(n-r)!



 = 





Factor out  n!/((n-r)!r!) and re-write:



 = 



= 



= 



=   ■







---------



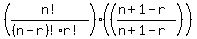
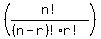
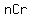(2) nPr = n!/(n-r)! = P(n,r)  <<< P(x,y) notation used below



    (n-r+1)*P(n,r-1)  



=    



=    



=    



=      ■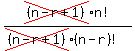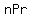