Question 1172438: Trish has a penny, 3 nickels, 4 dimes, and 3 quarters in her pocket. How many different arrangements are possible if she removes one coin at a time from her pocket? "46,200"
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
Edit: I'm redoing nearly the entire problem. Thanks ikleyn for pointing out I missed that penny. I'm not sure how I overlooked it.
Here's one way to approach the problem. We have 1+3+4+3 = 11 coins total. There are 11! = 39,916,800 ways to arrange them. The exclamation mark indicates factorial. We start at 11, and count our way down to 1, multiplying everything.
So,
11! = 11*10*9*8*7*6*5*4*3*2*1 = 39,916,800
This would be the answer if we could tell the nickels apart from other nickels, the dimes apart from the other dimes, and the quarters from the other quarters.
However, we cannot make such distinctions.
Since we cannot tell the nickels apart, this means we overcounted by a factor of 3! = 6 just for the nickels portion. Similarly, the dimes are overcounted by a factor of 4! = 24 as well. The quarters were overcounted by a factor of 3! = 6.
Overall, we overcounted by a factor of 6*24*6 = 864
We need to divide the result of the 11! by 864 to correct for this erroneous overcount.
Therefore, there are (11!)/(3!*4!*3!) = (39,916,800)/(864) = 46,200 distinct permutations possible.
Answer: 46,200
Answer by ikleyn(52788)  (Show Source):
You can put this solution on YOUR website! .
According to the condition, there is 1 (one) penny; 3 undistinguishable nickels; 4 undistinguishable dimes
and 3 undistinguishable quarters.
In all, there are 1 + 3 + 4 + 3 = 11 coins.
The number of distinguishable arrangements is
N = 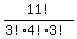 =  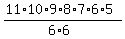= 46200,
which is exactly the number anticipated in your post.
Solved, answered and explained.
--------------
See the lesson
- Arranging elements of sets containing indistinguishable elements
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Combinatorics: Combinations and permutations".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|
