Question 1171151: How many solution does the equation  in integers between in integers between 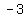 and and 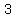 ? ?
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
****************************************************
The student responded to my original response saying that he wrote a computer program to find the correct answer, which he says is 224.
My original response was an attempt to show a solution using logical analysis and mathematics -- not a computer.
My approach was valid; but my counting of the number of ways was flawed. I have corrected those numbers and have come up with a new answer that agrees with his.
I have corrected my response below....
****************************************************
I was waiting to see if another tutor would come up with a clever way to find the answer....
Not seeing that happening, here is the solution I came up with....
-------------------------------------------------------------------
Use a "greedy" algorithm, where you make an ordered list with the entries higher in the list using more of the larger numbers.
To make sure you don't duplicate entries in the list, require that the four numbers be listed in non-increasing order.
Then, for each of the sets of 4 numbers you find, determine the number of different arrangements of those 4 numbers.
pattern requirement 4-tuples # of arrangements
-------------------------------------------------
(3,3,a,b): a+b=-5: (3,3,-2,-3)  12
(3,2,a,b): a+b=-4: (3,2,-1,-3) 12
(3,2,a,b): a+b=-4: (3,2,-1,-3)  24
(3,2,-2,-2) 24
(3,2,-2,-2)  12
(3,1,a,b): a+b=-3: (3,1,0,-3) 12
(3,1,a,b): a+b=-3: (3,1,0,-3)  24
(3,1,-1,-2) 24
(3,1,-1,-2)  24
(3,0,a,b): a+b=-2: (3,0,0,-2) 24
(3,0,a,b): a+b=-2: (3,0,0,-2)  12
(3,0,-1,-1) 12
(3,0,-1,-1)  12
(2,2,a,b): a+b=-3: (2,2,0,-3) 12
(2,2,a,b): a+b=-3: (2,2,0,-3)  12
(2,2,-1,-2) 12
(2,2,-1,-2)  12
(2,1,a,b): a+b=-2: (2,1,1,-3) 12
(2,1,a,b): a+b=-2: (2,1,1,-3)  12
(2,1,0,-2) 12
(2,1,0,-2)  24
(2,1,-1,-1) 24
(2,1,-1,-1)  12
(2,0,a,b): a+b=-1: (2,0,0,-1) 12
(2,0,a,b): a+b=-1: (2,0,0,-1)  12
(1,1,a,b): a+b=-1: (1,1,1,-2) 12
(1,1,a,b): a+b=-1: (1,1,1,-2)  4
(1,1,0,-1) 4
(1,1,0,-1) 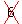 12
(1,0,a,b): a+b=0: (1,0,0,0) 4
------------------------------------------------------
total number of ways: 12
(1,0,a,b): a+b=0: (1,0,0,0) 4
------------------------------------------------------
total number of ways: 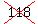 224 224
ANSWER: There are 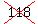 224 different ordered 4-tuples of integers between -3 and 3 with a sum of 1. 224 different ordered 4-tuples of integers between -3 and 3 with a sum of 1.
|
|
|