Question 1170031: There are 90 players in a league. Each of the 90 players plays exactly one match
against each of the other 89 players. Each match ends with a win for one player and
a loss for the other player, or with a tie for both players. Each player earns 1 point
for a win, 0 points for a loss, and 0.5 points for a tie. After all matches have been
played, the points earned by each player are added up. What is the greatest possible
number of players whose total score can be at least 54 points?
Answer by ikleyn(52943)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
There are 90 players in a league. Each of the 90 players plays exactly one match
against each of the other 89 players. Each match ends with a win for one player and
a loss for the other player, or with a tie for both players. Each player earns 1 point
for a win, 0 points for a loss, and 0.5 points for a tie. After all matches have been
played, the points earned by each player are added up. What is the greatest possible
number of players whose total score can be at least 54 points?
~~~~~~~~~~~~~
Imagine 90 x 90 matrix, to which you write the results of each match (game).
So, you write "1" into cell (i,j), if i-th player wins the game against j-th player;
you write "0" into cell (i,j), if i-th player loses the game against j-th player;
and you write "0.5" into cell (i,j) for a tie.
Notice that the sum of results in cells (i,j) and (j,i) is always 1.
Nobody plays against himself (herself); therefore, the diagonal cells (i,i) in our matrix are empty.
The sum of the values over all cells is, obviously,  = 45*89 = 4005.
Therefore, the number of those whose total score is at least 54 is no more than = 45*89 = 4005.
Therefore, the number of those whose total score is at least 54 is no more than 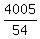 = 74.16.
Rounding to the nearest smaller integer number, we get the ANSWER 74. = 74.16.
Rounding to the nearest smaller integer number, we get the ANSWER 74.
Solved.
|
|
|