Question 1168473: In a class of 30 students 3 people are selected to be the line leader, the work collector, and the door holder. What is the probability of randomly selecting the correct students that have those jobs this week. (hint: does order matter? First find the combination or permutation [that is your denominator]. Your numerator is the # of correct options) WRITE YOUR ANSWER AS A FRACTION *
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you have 30 students.
you want to select 3 out of the 30.
each of the 3 will be the line leader, the work collector, and the door holder.
if you select the 3 without taking into consideration what job each will hold, then you would use the combination formula.
the combination formula is:
nCx or C(n,x) = n! / (x! * (n-x)!)
when n = 30 and x = 3, the formula becomes:
30C3 or C(30,3) = 30! / (3! * 27!)
this can be shown as:
30C3 or C(30,3) = (30 * 29 * 28 * 27!) / (3! * 27!)
either form, i.e., 30C3 or C(30,3) is acceptable and can be used.
they both reference the same formula.
the 27! in the numerator and denominator cancel out and you are left with:
30C3 or C(30,3) = (30 * 29 * 28) / (3 * 2 * 1)
solve for 30C3 or C(30,3) to get:
30C3 or C(30,3) = 4060.
the total number of possible combinations of sets of 3 elements each out of a set of 30 elements is 4060.
the probability of finding the correct 3 is 1 out of 4060 = 1/4060
if you are not considering which of the 3 is responsible for any of the positions, but just want to choose the who the 3 are, then the probability is 1 out of 4060 = 1/4060.
if you are looking for the correct 3 people and want to make sure those people are assigned to the correct position in the set of 3, then the formula becomes:
nPx or P(n,x)) = n! / (n-x)!
when n = 30 and x = 3, the formula becomes:
30P3 or P(30,3) = 30! / 27!
this can be shown as (30 * 29 * 28 * 27!) / 27!.
the 27! in the numerator and the denominator cancel out and you are left with:
30C3 or C(30,3) = 30 * 29 * 28 = 24360.
the probability of finding the correct 3 people is now 1 out of 24360 = 1/24360.
this is tough to show with finding 3 out of 30.
it can be shown with a smaller number, such as 3 out of 4.
with the combination formula, order is not important, so you are just looking for the 3 people regardless of what position they will hold.
4C3 or C(4,3) = 4
there are 4 possible sets of 3 that you can make out of a set of 4 where order is not important.
let the possible people be a,b,c,d
the 4 possible sets of 3 are:
a,b,c
a,b,d
a,c,d
b,c,d
if a,b,c are the correct people, then there is 1 correct set out of 4 for a probability of 1/4.
with the permutation, order is important, so you are looking for 3 people, each of whom will have a certain position.
let the first position in the set of 3 be the line leader and you want a to have that position.
let the second position in the set of 3 be the work collector and you want b to have that position.
let the third position in the set of 3 be the door holder and you want c to have that position.
4P3 or P(4,3) = 24
there are 24 possible sets of 3 out of a set of 4 that you can make where order is important.
they are:
abc
abd
acd
bcd
for each of those, there are 6 possible permutations.
for abc, they would be:
abc
acb
bac
bca
cab
cba
for abd, they would be:
abd
adb
bad
bda
cab
cba
for acd, they would be:
acd
adc
cad
cda
dac
dca
for bcd, they would be:
bcd
bdc
cbd
cdb
dbc
dcb
4 * 6 = 24 possible sets where order is important.
the correct set is abc, which is 1 out of the 24 for a probability of 1/24.
there is a calculator online that can do the combinations and permutations for you.
that calculator can be found at https://www.calculator.net/permutation-and-combination-calculator.html
you just enter the size of the set you are drawing from and the size of the sets you want to create and it tells you what the possible number of combinations and permutations are in one pass.
here's a display of the results of using that calculator for getting set of 3 out of 30 and for getting sets of 3 our of 4.
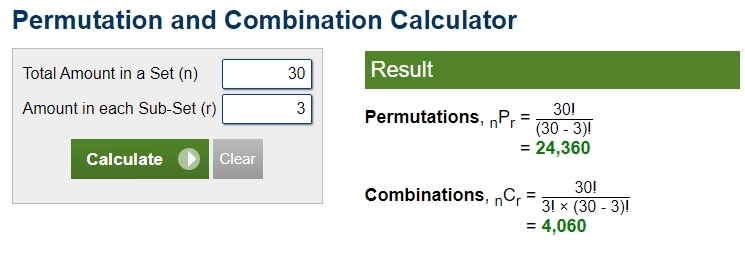
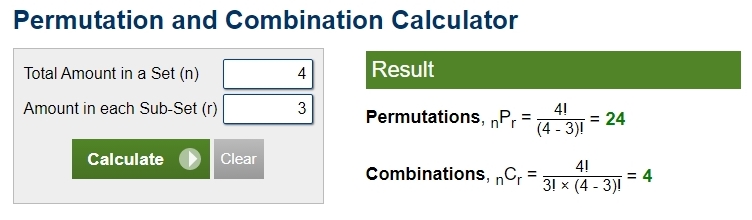
note that, with the combination formula, you got 1 set that had a,b,c in it.
with the permutation formula, you got 6 sets with abc in them.
those sets were abc, acb, bac, bca, cab, cba, but only one of those sets had abc in the correct position.
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In your post, what this passage means
. . . "randomly selecting the correct students" . . .
What are the INCORRECT students in this case ?
Formulated in this form, the post is not a Math question, at all.
-----------
Be sure, that I understand your question properly from its context;
but it is not a way to compose a Math problem.
In a true Math problem, its meaning should be clear from the text, not from the context.
|
|
|