Question 1168369: Hello,
My problem is detailed as below:
You have 9 different presents that each have to be given. They can either be given discreetly, (i.e. Give 1 of the 9 presents to someone), or some/all can be combined together and given (i.e. Give presents 1 and 2 to someone and 3-9 given discreetly all the way to giving all 9 presents combined to someone), but in each scenario, all 9 presents much be given.
How many total possible combinations are there? If you can help provide both the formula for arriving at the conclusion and the answer that would be much appreciated!
Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website! .
The problem in the post is given in a very uncertain mode/formulation.
I am not about more accurate wording, but about making a sense, in general.
Clearly, to be (to become) a real Math problem, it should be re-formulated.
It could be interpreted in this way.
9 different items should be distributed among n persons.
Each person can get one or more items, or can get no items, at all.
Find the number of different possible distributions.
I don't know if my interpretation is exactly what you keep in your mind.
But it is very nice Math problem from combinatorics.
1-st item can go to any of n persons (n options).
2-nd item can go to any of n persons (n options).
3-rd item can go to any of n persons (n options).
. . . . . . . . . . . . . . . . . . . . . . . . .
9-th item can go to any of n persons (n options).
In all, there are 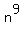 ways to distribute 9 items among n persons under given conditions. ANSWER
Solved.
|
|
|
