Question 1167300: a) How many seven-digit telephone numbers have one digit which is a multiple of 4 and six digits which are
not a multiple of 4?
b) How many seven-digit telephone numbers have three digits which are a multiple of 4 and four digits which
are not a multiple of 4?
c) Continuing the pattern, and adding the disjoint possibilities, answer the broader question: How many
seven-digit telephone numbers have exactly an odd number of digits which are a multiple of 4?
Answer by ikleyn(53411)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
a) How many seven-digit telephone numbers have one digit which is a multiple of 4 and six digits which are
not a multiple of 4?
b) How many seven-digit telephone numbers have three digits which are a multiple of 4 and four digits which
are not a multiple of 4?
c) Continuing the pattern, and adding the disjoint possibilities, answer the broader question: How many
seven-digit telephone numbers have exactly an odd number of digits which are a multiple of 4?
~~~~~~~~~~~~~~~~~~~~~~~~~
(a) There are 7 possible positions for one digit which is multiple of 4.
It gives us the factor (multiplier) 7.
There are 3 possibilities for a digit multiple of 4: '0', '4', '8'.
It gives us the factor (multiplier) 3.
In the rest 6 positions, we may have any of 10-3 = 7 digits 1, 2, 3, 5, 6, 7, 9 independently.
It gives us the factor (multiplier)  .
Thus the ANSWER to question (a) is the product of factors .
Thus the ANSWER to question (a) is the product of factors 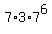 = = 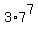 = 2,470,629.
Part (a) is complete.
(b) Three digits which are multiple of 4, can be placed in = 2,470,629.
Part (a) is complete.
(b) Three digits which are multiple of 4, can be placed in  = = 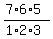 = 7*5 = 35 different ways.
These three digits can be 0, 4, 8 independently.
So far, we have the multiplier = 7*5 = 35 different ways.
These three digits can be 0, 4, 8 independently.
So far, we have the multiplier 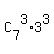 = 35*9.
The remaining 4 digits are in the remaining positions.
These remaining digits can be any of 10-3 = 7 digits 1, 2, 3, 5, 6, 7, 9.
It gives us the multiplier = 35*9.
The remaining 4 digits are in the remaining positions.
These remaining digits can be any of 10-3 = 7 digits 1, 2, 3, 5, 6, 7, 9.
It gives us the multiplier  .
Thus the ANSWER to question (b) is the product of factors .
Thus the ANSWER to question (b) is the product of factors 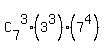 = 35*(3^3)*(7^4) = 2268945.
Part (b) is complete. = 35*(3^3)*(7^4) = 2268945.
Part (b) is complete.
---------------------------------------
Thus parts (a) and (b) are just solved.
With it, you got from me the idea how to solve for one special digit and for 3 special digits.
The move forward for 5 special digits and for 7 special digits is very similar to it.
So, from my post, you just have and idea.
I will stop at this point and will not solve (c) in order for do not turn my post into mess.
Continue in the same manner to complete for part (c).
|
|
|