SOLUTION: Susie has three identical apples, three identical oranges and three identical pears. She wants to create a straight line arrangement using six of these pieces of fruit for an art

We should consider SEVERAL different cases.


Case 1).  There are 1 apple, 2 oranges and 3 pears among the selected 6 pieces of fruit
          Short signature is (1a, 2o, 3p).

      +------------------------------------------------------------------------------------------------+
      |   and 5 other "isomorphic" cases, making all possible 6 (six) permutations of this signature    |
      +------------------------------------------------------------------------------------------------+


Case 2).  There are 3 apples, 1 orange and 2 pears among the selected 6 pieces of fruit.
          Short signature is (3a, 1o, 2p).


Case 3).  There are 2 apples, 3 oranges and 1 pear among the selected 6 pieces of fruit.
          Short signature is (2a, 3o, 1p).


Case 4).  There are 3 apples, 2 oranges and 1 pear among the selected 6 pieces of fruit.
          Short signature is (3a, 2o, 1p).


Case 5).  There are 1 apple, 3 oranges and 2 pears among the selected 6 pieces of fruit.
          Short signature is (1a, 3o, 2p)


Case 6).  There are 2 apples, 1 orange and 3 pears among the selected 6 pieces of fruit.
          Short signature is (2a, 1o, 3p).


Case 7).  There are 2 apples, 2 oranges and 2 pears among the selected 6 pieces of fruit.
          Short signature is (2a, 2o, 2p).
          For this signature, all other permutations are identical and, therefore, are not considered.


Case 8).  There are 3 apples and 3 oranges.
          Short signature is (3a, 3o, 0p).

      +--------------------------------------------------------------------------------------------------+
      |   and 2 other "isomorphic" cases, making all possible 3 (three) permutations of this signature    |
      +--------------------------------------------------------------------------------------------------+


Case 9).  There are 3 apples and 3 pears.
          Short signature is (3a, 0o, 3p).


Case 10). There are 3 oranges and 3 pears.
          Short signature is (0a, 3o, 3p).


It is clear that

    a)  all these 10 cases produce DIFFERENT sequences of 6 fruits, ordered in the line;

    b)  "isomorphic" cases 1) - 6)  produce EQUAL number of different 6-piece sequences

              so, calculating these 6 cases, it is enough to calculate the number of sequences for any one single signature
              and then multiply it by 6 in the total sum;

    c)  "isomorphic" cases 8) - 10)  produce EQUAL number of different 6-piece sequences

              so, calculating these 3 cases, it is enough to calculate the number of sequences for any one single signature
              and then multiply it by 3 in the total sum.


Now, the number of all different linear sequences for case 1) is   = 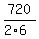 = 60.

     I use the WELL KNOWN formula for arrangements of 6 items with 2 and 3 undistinguishable items.



Next, the number of all different linear sequences for case 7) is 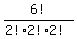  = 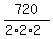 = 90.

     I use the SIMILAR formula for arrangements of 6 items with 2, 2 and 2 undistinguishable items.



Finally, the number of all different linear sequences for case 8) is 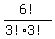  = 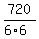 = 20.



After that, taking into account everything that was said above, the final answer is


    N = 6*60 + 90 + 3*20 = 510.


ANSWER.  The total number of all different linear sequences (arrangements) in this problem is 510.