Question 1162656: The positive integers 1,2,3,4,...,m are written one after another to form the integer L = 123456789101112131415 . . .. What is the smallest integer m > 2020 for which L is divisible by 9?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(1) A number is divisible by 9 if the sum of its digits is divisible by 9.
(2) We can ignore the 0's in the number, since they add nothing to the sum of the digits.
(3) The number 123456789 is divisible by 9, because the sum of the digits is 45, which is divisible by 9.
So the number L is divisible by 9 through m=9.
(4) In the number 101112...979899, the digits 1 through 9 are each used the same number of times, so the sum of the digits is a multiple of the sum of the digits 1 through 9, which is divisible by 9.
So the number 101112...979899 is divisible by 9; and so the number L through m=99 is divisible by 9.
(5) The same argument holds for the number 100101102...997998999 -- each digit 1 through 9 is used the same number of times, so the number 100101102...997998999 is divisible by 9.
So the number L through m=999 is divisible by 9.
(6) For the number 100010011002...199719981999, we again have the same digits as in the number 123456789101112...997998999, plus we have 1000 1's. Those 1000 1's have a sum of 1000, which is 1 more than a multiple of 9.
So the number L through m=1999 has remainder 1 when divided by 9.
From here, it looks as if we need to go one more number m at a time in order to find the first one larger than 2020 for which the integer L is divisible by 9.
(perhaps another tutor will respond showing an easier way to get from here to the answer -- or perhaps to solve the whole problem more easily)
We start knowing that through m=1999 the integer L has remainder of 1 when divided by 9 -- i.e., L = 1 mod 9.
We go from there, remembering that we are looking for the first m greater than 2020 for which L is divisible by 9....
m added
sum L mod 9
-------------------
2000 2 3
2001 3 6
2002 4 10 = 1
2003 5 6
2004 6 12 = 3
2005 7 10 = 1
2006 8 9 = 0
2007 9 9 = 0
2008 10 10 = 1
2009 11 12 = 3
2010 3 6
2011 4 10 = 1
2012 5 6
2013 6 12 = 3
2014 7 10 = 1
2015 8 9 = 0
2016 9 9 = 0
2017 10 10 = 1
2018 11 12 = 3
2019 12 15 = 6
2020 4 10 = 1
2021 5 6
2022 6 12 = 3
2023 7 10 = 1
2024 8 9 = 0
ANSWER: m=2024 is the smallest integer greater than 2020 for which L is divisible by 9.
Note that, from the pattern of L mod 9 for m from 2000 to 2020, we could have predicted the answer; but since the period of the pattern is relatively short it was just as easy to continue with the table.
Cool problem....
I will be looking to see if another tutor has an elegant way of finding the answer with less effort.
-----------------------------------------------------------
Thanks to tutor @ikleyn for showing a much easier path to the answer to the problem....
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Here is another ("elegant") solution, which tutor @greenestamps wants to see
(and you, probably, too).
The base for this solution is the same rule of divisibility by 9:
The number is divisible by 9 if and only if the sum of its digits is divisible by 9.
The more general form of this rule is
For any number, the remainder of dividing by 9 is the same as the remainder of dividing by 9 the sum of its digits.
For both forms, see the lesson
- Divisibility by 9 rule
in this site.
It follows immediately from these rules, that the remainder of division the number L(m) by 9
is equal to the remainder of divisibility by 9 the number
1 + 2 + 3 + . . . + 9 + 10 + 11 + 12 + . . . + 99 + 100 + 101 + 102 + . . . 999 + 1000 + 1001 + 1002 + . . . + the last 4-digit number m =
= the sum of the first "m" natural numbers = 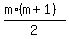 .
So, all we need is to check the remainder of dividing by 9 of several numbers of the form .
So, all we need is to check the remainder of dividing by 9 of several numbers of the form 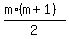 ,
starting from m = 2021, 2022, 2023, 2024 . . .
The table below (made using the function r = mod(N,9) of Excel) shows these remainders
m 2021 2022 2023 2024
r = ,
starting from m = 2021, 2022, 2023, 2024 . . .
The table below (made using the function r = mod(N,9) of Excel) shows these remainders
m 2021 2022 2023 2024
r = 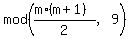 6 3 1 0
Thus that minimal value of "m" the problems is asking for is 2024. ANSWER 6 3 1 0
Thus that minimal value of "m" the problems is asking for is 2024. ANSWER
Solved.
|
|
|