Question 1159622: How many ways can you order the letters of TORONTO if you must begin with exactly 2 O's?
Found 3 solutions by KMST, ikleyn, greenestamps:
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! IF you place two of the O's first, you have  letters left: T, T, R, N and O.
FIVE-LETTER SEQUENCES FORMED WITH two (different) T's, R, N and O:
There are  ways to arrange different letters.
However, to have exactly two O's at the beginning, we only want the arrangements of those 5 letters that do not start with O.
There are  of the total, or  that start with O,
and there is also 24 that start with each (different) T, 24 that start with N, and 24 that start with R.
If the two T's were marked so as two distinguish between them (for example, different colors), you would have a total of  different arrangements of those letters, including the ones that start with O.
There are of the total, or that start with O,
and there is also 24 that start with each (different) T, 24 that start with N, and 24 that start with R.
Of that total there are  that do not start with O.
FIVE-LETTER SEQUENCES FORMED WITH two (identical) T's, R, N and O:
However, if the two T's are identical, you would see only  different sequences that do not start with O, each of them duplicated, 12 that start with N, 12 that start with R and 24 that start with T.
SEVEN-LETTER SEQUENCES starting with exactly two O's formed from two (identical) T's, R, N and three (identical) O's:Assuming that there is no way to distinguish one T from another T and one O from another O, you could form  distinguishable letter sequences.
If the different T's and the different O's were marked so as to distinguish them, you would have  ways to choose the first and second O,
and then 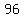 ways two arrange the remaining letters,
for a total of  different sequences starting with exactly
two O's
Answer by ikleyn(52780)  (Show Source):
You can put this solution on YOUR website! .
As the problem is worded, it is UNCLEAR if " O " can be / (or can not be) third letter.
It depends on interpretation; but everything that depends on interpretation --- is not a Math problem.
It is "a puzzle", in a bad sense of this term; but NOT a Math problem.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
The number of ways to arrange the letters to begin with EXACTLY two O's is the total number of ways to arrange the letters beginning with AT LEAST 2 O's, minus the number of ways to arrange them starting with 3 O's.
The number of ways to arrange the letters starting with AT LEAST 2 O's is the number of ways of arranging the letters TRNTO, which is 
The number of ways of arranging the letters starting with 3 O's is the number of ways of arranging the letters TRNT, which is  .
The number of ways of arranging the letters starting with EXACTLY 2 O's is 60-12 = 48.
ANSWER: 48 ways to arrange the letters of TORONTO starting with exactly two O's.
|
|
|
