Question 1154708: From a standard pack of 52 cards, three cards are selected at random. If the cards are selected from the pack one at a time and each card is replaced before the next one is drawn, what is the probability that they are the jack of spades, the two of clubs and the seven of diamonds?
The answer is  .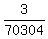
My working out was along the lines of this:
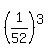
Found 2 solutions by Alan3354, greenestamps:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! From a standard pack of 52 cards, three cards are selected at random. If the cards are selected from the pack one at a time and each card is replaced before the next one is drawn, what is the probability that they are the jack of spades, the two of clubs and the seven of diamonds?
The answer is .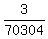
========================
Call the 3 cards a, b & c (to save typing)
Since no order of the 3 cards being drawn, the draws can be
a, b, c
a, c, b
b, a, c
etc
---> 6 possible combinations
------------
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
Your answer of (1/52)^3 is the probability of getting the the jack of spades, the two of clubs and the seven of diamonds IN THAT ORDER.
But those three cards can be drawn in any one of 3*2*1 = 6 orders.
ANSWER: 6*(1/52)^3 = 3/70304
|
|
|
