SOLUTION: x1 + x2 + x3 + x4 + x5 = 36 How many solutions (using only nonnegative integers) are there to the following equation?

x1 + x2 + x3 + x4 + x5 = 36     (1)


Imagine 36 marbles on the table, placed in one straight line with small gaps between them.


Imagine you have 6 numbered bars, of which you place the first bar (bar N1) before the first marble and the last bar (bar N6) 
after the last marble in the row.


Let  , ,  , ,  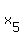be some solution to the given equation.


You then place bar N2 after -th marble in the gap in the row of marbles; 

then you count next  marbles  in the row of marbles after bar N2 and place bar N3 in the gap there;

then you count next  marbles  in the row of marbles after bar N3 and place bar N4 in the gap there;

finally, you count next  marbles  in the row of marbles after bar N4 and place bar N5 in the gap there.


At this moment, all 36 marbles are divided in 5 groups between bars (1-2), (2-3), (3-4), (4,5) and (5,6).


Notice that if some  is zero, then the corresponding bars go to common respective gap.


So, having the solution to equation (1) in non-negative positive integer number, you place 4 bars N2, N3, N4 and N5 in 
their corresponding positions in gaps in the row of marbles. 


Vise versa, if you place 4 bars B2, B3, B4 and B5 in gaps in the row of 36 marbles, you divide marbles in 5 groups, 
and the numbers of marbles in each group form the solution to equation (1).


Thus, there is one-to-one correspondence between the set of solutions to equation (1) in non-negative integer numbers, 

from one side, and all different possible placings of 4 bars in 35 gaps in the row between 36 marbles.


Thus we have 35+4 = 39 entities, 35 marbles and 4 bars; 35 marbles are indistiguishable and 4 movable bars 
are indistinguishable, too.


The number of all possible indistinguishable arrangements of 39 items of two types with 35 indistinguishable of one type 

and 4 indistinguishable of the other type is 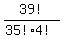  = 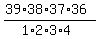 = 82251.


Hence,  the number of all possible solutions to equation (1) in non-negative integer numbers is equal to 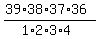  = 82251.   

ANSWER.  The number of different solutions to equation (1)  is  82251.

More general problem to find the number of non-negative integer solution to equation

     +  +  + . . . +  = n    

where k <= n, can be solved in the same way and has the answer  .


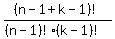We have then   (n-1)  gaps between  "n"  "marbles"  and  (k-1)  movable dividing bars.


The method I used in the solution is called the  "method of bars and stars".


You can read about it in this Wikipedia article

https://en.wikipedia.org/wiki/Stars_and_bars_%28combinatorics%29