Question 1149518: Find how many groups of one or more digits can be formed from the following digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 if repetition is not allowed
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website! .
It is THE SAME as to ask: how many subsets, containing one or more items, can be formed from 10 items.
The answer is VERY WELL known.
The number of ALL subsets of the set containing "n" elements is  .
One of this sets is empty, which is not considered (not allowed) in this problem.
So, the final answer is 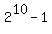 = 1024 - 1 = 1023 subsets.
Solved, answered and explained. And completed.
-----------
Look into the lesson
- How many subsets are there in a given finite set of n elements?
in this site, written specially for those who meet and see such problem for the first time in their life.
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
The question is equivalent to asking how many non-empty subsets there are of a set with 10 elements.
The number of subsets of a set with n elements, including the empty set, is 2^n; and obviously there is only 1 empty subset. So
ANSWER: 2^10-1 = 1023
You can also look at finding the answer as
C(10,1)+C(10,2)+...+C(10,9)+C(10,10) = 2^10 - C(10,0) = 2^10-1 = 1023
|
|
|
