Question 1149503: A committee of 5 people is selected from a group of 7 men and 8 women. In how many ways can the committee be selected so it contains at least 1 woman?
Answer by ikleyn(52925)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In all, there are 7+8 = 15 individuals,
and 5 people of 15 can can be selected in 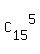 ways.
It is the total possible number of groups of 5 individuals.
Now, the committee of 5 people, consisting of men ONLY, can be selected in ways.
It is the total possible number of groups of 5 individuals.
Now, the committee of 5 people, consisting of men ONLY, can be selected in  ways.
The answer to the problem question is the COMPLEMENT of ways.
The answer to the problem question is the COMPLEMENT of  to to 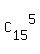 , i.e. the difference , i.e. the difference 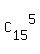 - -  .
You do the calculations, following my instructions. .
You do the calculations, following my instructions.
Answered.
Shortly speaking, from the number of all possible groups of 5 I subtracted the number of such groups consisting of men only.
-----------------
On Combinations, see introductory lessons
- Introduction to Combinations
- PROOF of the formula on the number of Combinations
- Problems on Combinations
- OVERVIEW of lessons on Permutations and Combinations
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Combinatorics: Combinations and permutations".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|