Question 1148437: A group of 7 people are to be put into a line. Among these people are Doc, Frank and Shem. What is the probability that the 1st 3 people in order are Doc, Frank and Shem?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In all, there are 7! permutations of 7 different items (persons, in this case).
Of these permutations, favorable are those, which start with Doc, Frank and Shem, in this order.
The number of favorable permutations is (7-3)! = 4!
Therefore, the probability under the question is
P = 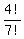 = = 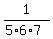 = = 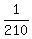 . ANSWER . ANSWER
Solved, answered and explained. And completed.
-----------------
On Permutations, see introductory lessons
- Introduction to Permutations
- PROOF of the formula on the number of Permutations
- Problems on Permutations
- OVERVIEW of lessons on Permutations and Combinations
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Combinatorics: Combinations and permutations".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
For finding the probability in this simple problem, there are simpler methods for than shown by tutor @ikleyn. However, you should understand the method she shows, because it will be needed when the problems are more complicated.
The alternative to her method is to look separately at the probabilities of each person getting in the correct position in the line.
P(Doc is 1st) = 1/7
P(Frank is 2nd) = 1/6
P(Shem is 3rd) = 1/5
P(Doc 1st AND Frank 2nd AND Shem 3rd) = (1/7)(1/6)(1/5) = 1/210
|
|
|