Question 1147274: Four adults are standing in a room that has five exits. Each adult is equally likely to leave the room through any one of the five exits.
b)What is the probability that three particular adults use the same exit and the fourth adult uses a different exit?
c) What is the probability that any three of the four adults come out the same exit, and the remaining adult comes out a different exit?
d) What is the probability that no more than two adults come out any one exit?
Thank you in advance!!!
Answer by VFBundy(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! b)What is the probability that three particular adults use the same exit and the fourth adult uses a different exit?
Three PARTICULAR adults means three specific adults, and not just any three adults. So, let's say Adults A, B, and C use the same exit and the remaining adult (D) uses a different exit. It should also be noted that, while three particular adults use the same exit, the exit itself is not particular.
Probability Adult A, B, and C use Exit 1, and Adult D uses another exit: 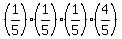 = 4/625 = 4/625
Probability Adult A, B, and C use Exit 2, and Adult D uses another exit: 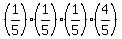 = 4/625 = 4/625
Probability Adult A, B, and C use Exit 3, and Adult D uses another exit: 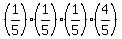 = 4/625 = 4/625
Probability Adult A, B, and C use Exit 4, and Adult D uses another exit: 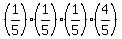 = 4/625 = 4/625
Probability Adult A, B, and C use Exit 5, and Adult D uses another exit: 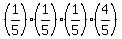 = 4/625 = 4/625
Add all of these results together to get: 20/625 = 4/125
=================================================================
c) What is the probability that any three of the four adults come out the same exit, and the remaining adult comes out a different exit?
Unlike the first problem, this is asking what the probability is that ANY three adults use the same exit.
Probability any three adults use Exit 1 and the remaining adult uses another exit: 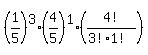 = 16/625 = 16/625
Probability any three adults use Exit 2 and the remaining adult uses another exit: 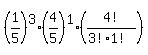 = 16/625 = 16/625
Probability any three adults use Exit 3 and the remaining adult uses another exit: 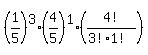 = 16/625 = 16/625
Probability any three adults use Exit 4 and the remaining adult uses another exit: 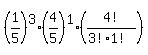 = 16/625 = 16/625
Probability any three adults use Exit 5 and the remaining adult uses another exit: 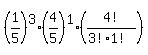 = 16/625 = 16/625
Add all of these results together to get: 80/625 = 16/125
=================================================================
d) What is the probability that no more than two adults come out any one exit?
To do this, we need to figure out what the probability of the opposite is...what is the probability that three or more adults come out any one exit? Or, to put it another way, the probability that exactly three adults come out any one exit PLUS the probability that all four of the adults come out any one exit.
As luck would have it, we've already figured out what the probability is that exactly three adults would come out any one exit, in Part C above. That answer is: 16/125.
So, we now need to figure out what the probability is that all four adults use any one exit.
Probability all four adults use Exit 1: 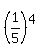 = 1/625 = 1/625
Probability all four adults use Exit 2: 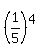 = 1/625 = 1/625
Probability all four adults use Exit 3: 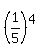 = 1/625 = 1/625
Probability all four adults use Exit 4: 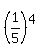 = 1/625 = 1/625
Probability all four adults use Exit 5: 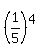 = 1/625 = 1/625
Add all these results together to get: 5/625 = 1/125.
So, the probability that all four adults use any one exit is 1/125. As noted earlier, we already know the probability that exactly three adults use the same exit is 16/125. So, to figure out the probability that three or more adults come out any one exit, add these two results together: 1/125 + 16/125 = 17/125.
However, the question asked us what the probability is that no more than two adults come out the same exit. We just figured out what the probability is that three or more adults come out of the same exit (17/125), so the probability that no more than two adults come out of the same exit is: 1 - 17/125 = 108/125
|
|
|