Question 1145099: You are given 25 video game tokens to use on these three games: Radical Racing Robots, Adventures Around the Amazon, and Mighty Medical Monsters. In order to get your prize, you must correctly answer this question:How many different ways are there to spend your 25 tokens on these three games assuming you play each game at least once?
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The answer is the number of solutions of the equation

where a, b, and c are positive integers.
Problems like that can be solved using a method popularly known as "stars and bars". Let's look at solving your problem using this method where the number of tokens is 5 instead of 25.
We start by assigning 1 token to each of the 3 games. That done, we have satisfied the requirement of playing each game at least once, and we are now left with 2 tokens to use on any games we want.
Now we use the stars and bars technique.
Represent the two remaining tokens with stars:
**
To represent dividing those two tokens among the 3 games, use two separator symbols "|"; the two separator symbols will divide the stars into 3 groups.
For example,
*||* represents playing games 1 and 3 once each with the remaining 2 tokens;
|**| represents playing game 2 with both of the remaining tokens
The number of different ways of distributing the two remaining tokens is then the number of distinct ways of arranging the "stars and bars" ||**.
By a well known counting principle, that number of ways is

So in our smaller problem, the number of ways of using 5 tokens to play the three games, playing each game at least once, is 6.
For your problem, with 25 tokens, we again use 3 of them to make sure we play each of the 3 games at least once. Then we are left with 22 tokens (stars) to be divided among 3 games using 2 divider symbols (bars); and the number of ways to divide the 25 tokens among the 3 games playing each game at least once is determined using 25-3=22 stars and 2 bars:

The stars and bars method can be used on a large number of problems where the solution can be modeled by an equation of the form a+b+c+...=N where N is an integer total and the variables a, b, c,... are non-negative integers.
The most common other kind of problem like this, in my experience, is finding the number of terms in the expansion of a polynomial. As an example, of that, here is a problem that uses the same numbers as in your problem:
Find the number of terms in the simplified form of 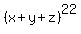
In each term of the expansion, the exponents are all integers, and the sum of the exponents is 22. So again we have a problem where the answer is the number of non-negative integer solutions of the equation a+b+c=22.
So again we have a case of 22 "stars" (the exponents) being divided into 3 groups (the variables x, y, and z) by 2 separator symbols ("bars"). And so, like your problem, the answer to this problem would be

|
|
|