Question 1140715: A box contains 5 blue,7 green and 4 red identical balls. Three balls are picked from the box one after the other without replacement. Find,the probability of picking:
(a) two green balls and a blue ball;
(b) no blue ball;
(c) at least one green ball;
(d) three balls of the same color.
NB: please use combination approach.
Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!
In each case, you are picking 3 of the 16 balls, so the denominator of the probability fraction is  .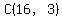
(a) 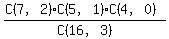 2 of the 7 green, 1 of the 5 blue, and 0 of the 4 red
(b) 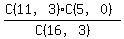 3 of the 11 green or red, 0 of the 5 blue
(c) 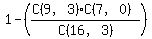 NOT 3 of the 9 red or blue and 0 of the 7 green
(d)  3 of the 5 blue, OR 3 of the 7 green, OR 3 of the 4 red
NOTE: In case (a), it was not necessary to include C(4,0) in the calculation to indicate that no red balls were chosen. However, especially when you are first learning to work combination problems like this, it is helpful to see that in every case the sums of the numbers in the numerator are equal to the numbers in the denominator.
Specifically, in this case, including C(4,0) in the calculation gives us 7+5+4=16 and 2+1+0=3. That gives you reassurance that the numbers you are using are valid.
|
|
|
