Question 1140059: ’╝ł1’╝ēin how many ways can 4 boys and 3 girls be arrange in a line if the 3 girls are to be seperated
’╝ł2’╝ēwhen the number of the ways permuting the letters "HELL" such that ’╝łA’╝ē2ls well always be together ’╝łB’╝ēthe 2ls will always be apart.
Found 2 solutions by KMST, ikleyn:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! (1) I would start by numbering the positions in the line as positions 1 through  . .
Then I would try to decide what positions to give the girls. If position 1 would go to a girl, I cannot place a girl in position 2, but a second girl could take position 3, and then maybe I can give position 5 to a the remaining girl. That would be a 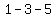 set of positions. set of positions.
Other choices for position sets for the girls are:
 , , 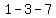 , , 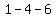 , ,  , ,  , ,
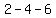 , ,  , , 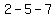 , ,
and 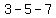 . .
That is  different sets of positions that could be reserved for the girls. different sets of positions that could be reserved for the girls.
For each of those  different options, I can still decide which girl goes first, second, and third. That gives us another set of different options, I can still decide which girl goes first, second, and third. That gives us another set of  girl ordering options (independently of the position arrangement), and girl ordering options (independently of the position arrangement), and
 different ways arrange the girls. different ways arrange the girls.
That still leaves us the choice of how to arrange the 4 boys in the 4 empty positions. There are  different ordering ways to arrange the boys. different ordering ways to arrange the boys.
That gives us a total of  different ways to arrange 4 boys and 3 girls in a line if the 3 girls are to be separated. different ways to arrange 4 boys and 3 girls in a line if the 3 girls are to be separated.
(2) (A) Assuming which L appears first does not matter (because maybe we cannot tell them apart), there would be  ways to arrange 3 tiles labelled H, E. and LL: ways to arrange 3 tiles labelled H, E. and LL:
H E LL, H LL E, E H LL, E LL H, LL E H, and LL H E.
(2) (B) To get the two L's separated we can have them either as the first and third letter, or as the second and fourth letter. That gives us two different options. That is  choices for placement of the L's. choices for placement of the L's.
For each of those options we can choose to either have the H before the E, or the E before the H. That is  choices independent of the L-placement options. choices independent of the L-placement options.
So assuming that we cannot tell the L's apart, there would be  "words" we could form: "words" we could form:
LHLE, LELH, HLEL, and ELHL .
(2) NOTE: If we could tell apart the L's, the number of arrangements would be double, because either one or the other L could go first.
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The correct answer to question (B) of (2) is 6.
The six arrangements are LHLE, LELH, HLEL, ELHL, LHEL and LEHL.
The two last arrangements, that are underlined, are those missed by tutor @KMST.
|
|
|