Question 1136227: A train going from cambridge to London stops at 9 intermediate station.Six person enter the train during the journey with 6 different tickets of the same class.How many different sets of tickets would they hsve?
Answer by ikleyn(52778)   (Show Source):
You can put this solution on YOUR website! .
I am not familiar with this train root and don't know exactly how many stops
are there from Cambridge to London.
And the problem do not point it exactly. So I will assume
that there are 9 stations, counting from the next from Cambridge to London INCLUSIVELY.
Also, I will assume that all 6 persons entered at Cambridge, but are free to leave the train at any other station.
If it is not so, then my solution needs to be corrected. (Sorry)
Of 6 persons entering at Cambridge, each is free to have a ticket to any of 9 stations.
It gives 9 opportunities in each of 6 positions; so, there are 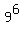 different sets of tickets possible. ANSWER
I can reformulate this problem in other form:
Let 9 letters A, B, C, D, E, F, G, H, I represent the names of the stations starting from next after Cambridge to London inclusively.
Then every of 6 person may have in his hand any of these 9 letters as his ticket.
Then the problem's question is: how many 6-letter words do exist written in this 9-letter alphabet.
The ANSWER is 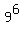words.
The same answer as in the previous solution.
Surely, both solutions are the same, simply expressed in different terms.
Solved.
My opinion is that this problem (to be in style of Conan Doyle's Sherlock Holmes and Dr. Watson) could be
(and should be) formulated in more precise terms . . .
--------------
To see other similar problem solved, look into the lesson
- Combinatoric problems for entities other than permutations and combinations, Problem 7
in this site.
|
|
|
