.
The formulation of this post seems to be tricky, so we need re-formulate it in clean, clear and simple form.
The 4 papers can be checked by any team of 4 teachers; by any team of 3 teachers; by any team of 2 teachers;
and, finally, by any one of 7 teachers.
So we need to calculate the sum
sum = 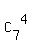 +
+  +
+  +
+ 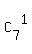 (which is the number of elements in the space of events)
and then calculate the probability as the ratio P =
(which is the number of elements in the space of events)
and then calculate the probability as the ratio P = 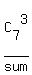 , where
, where  is the number of favorable events.
In this way we will get the answer.
is the number of favorable events.
In this way we will get the answer.
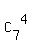 =
= 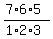 = 35;
= 35;
 =
= 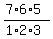 = 35;
= 35;
 =
=  = 21;
= 21;
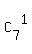 = 7.
So, sum = 35 + 35 + 21 + 7 = 98.
Therefore, P =
= 7.
So, sum = 35 + 35 + 21 + 7 = 98.
Therefore, P = 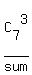 =
= 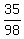 =
= 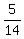 .
Since we are given that P =
.
Since we are given that P = 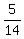 =
= 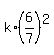 , it implies
k =
, it implies
k = 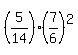 =
= 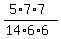 =
= 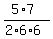 =
= 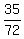 . ANSWER
ANSWER. k =
. ANSWER
ANSWER. k = 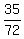 .
.
SOLVED.