Question 1134889: If 8 teachers are to be divided among 4 schools, how many divisions are possibles?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
This problem has FANTASTICALLY beautiful solution.
Consider the linear expression X + Y + Z + W of four variables X, Y, Z and W, and consider its 8-th degree  .
If you FOIL this expression and collect like terms, you will get the sum .
If you FOIL this expression and collect like terms, you will get the sum
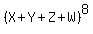 = =  . (1)
consisting of monoms . (1)
consisting of monoms 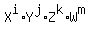 with integer coefficients C(i,j,k,m) that depend on the sets of non-negative integer indexes (i, j, k, m).
The sum (1) is spread (is distributed) over all such sets of non-negative integer indexes that i+j+k+m = 8.
We can interpret each monom with integer coefficients C(i,j,k,m) that depend on the sets of non-negative integer indexes (i, j, k, m).
The sum (1) is spread (is distributed) over all such sets of non-negative integer indexes that i+j+k+m = 8.
We can interpret each monom 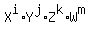 (or each set (i,j,k,n) ) as a distribution sample of 8 teachers (= 8 objects)
i teachers in the school X;
j teachers in the school Y;
k teachers in the school Z and
m teachers in the school W
among 4 school (=4 boxes). Doing in this way, we do not personalize the teachers - we distinct and consider only "signatures" (i,j,k,n),
attaching and connecting them to school X, Y, Z and W.
But if we personalize the teachers, we will get the coefficients C(i,j,k,m) showing HOW MANY personalized combinations of teachers
we will have for each given signature (i,j,k,m).
So, each given coefficient C(i,j,k,m) shows how many personalized combinations are there for each given numerical signature (i,j,k,m).
But in this problem we are not interested in knowing each and every coefficient C(i,j,k,m) individually and separately -
we are interested only to know the sum of all coefficients C(i,j,k,m).
The last observation is that this sum is nothing else as the value of (or each set (i,j,k,n) ) as a distribution sample of 8 teachers (= 8 objects)
i teachers in the school X;
j teachers in the school Y;
k teachers in the school Z and
m teachers in the school W
among 4 school (=4 boxes). Doing in this way, we do not personalize the teachers - we distinct and consider only "signatures" (i,j,k,n),
attaching and connecting them to school X, Y, Z and W.
But if we personalize the teachers, we will get the coefficients C(i,j,k,m) showing HOW MANY personalized combinations of teachers
we will have for each given signature (i,j,k,m).
So, each given coefficient C(i,j,k,m) shows how many personalized combinations are there for each given numerical signature (i,j,k,m).
But in this problem we are not interested in knowing each and every coefficient C(i,j,k,m) individually and separately -
we are interested only to know the sum of all coefficients C(i,j,k,m).
The last observation is that this sum is nothing else as the value of 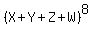 at X= 1, Y= 1, Z=1 and W= 1.
Thus the sum of all coefficients at X= 1, Y= 1, Z=1 and W= 1.
Thus the sum of all coefficients
 = = 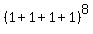 = = 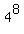 .
And it gives the ANSWER to the problem's question:
There are .
And it gives the ANSWER to the problem's question:
There are 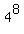 ways to distribute 8 teachers among 4 school. ways to distribute 8 teachers among 4 school.
Solved, completed, answered and explained.
-------------
For more general problem
In how many ways N distinguishable objects can be distributed among n different boxes
the solution and the answer are similar: in 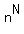 ways. ways.
This problem is, obviously, far above the average school level.
It is typical problem of the Math Circle level at a respectful university.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The statement of the problem is sufficiently unclear that different interpretations are possible.
If the 8 teachers are individually identifiable, then each of the 8 teachers has 4 possibilities of which school to be assigned to; the "number of divisions" is then 4^8.
A more common (and more interesting) problem is with the 8 teachers NOT individually identifiable, and the "number of divisions" is the number of different ways the 4 schools can get certain numbers of teachers -- for example, 3 teachers to school A, none to school B, 1 to school C, and 4 to school D.
So this kind of problem is one in which, if we let A, B, C, and D represent the numbers of teachers assigned to each school, we are looking for the number of solutions in whole numbers of the equation

This kind of equation comes up in a large number of similar types of problems. A well-known method for solving them is "stars and bars".
With the stars and bars method, you start with 8 stars, representing the 8 teachers to be divided among the schools:
* * * * * * * *
To divide the teachers among the four schools, you add THREE bars as separator symbols; for example
* * | * * | * * | * * (2 teachers to each of the 4 schools)
* * * | | * | * * * * (3; 0; 1; and 4}
* | * * * | * | * * * (1; 3; 1; and 3)
Each different placement of the 3 separator symbols -- i.e., each different arrangement of the 8 stars and 3 bars -- represents one of the possible ways to divide the 8 teachers among the 4 schools.
By a well known counting principle, that number of different arrangements is

...a vastly different answer with this interpretation of the problem...!
|
|
|