.
From the dictionary
https://dictionary.cambridge.org/us/dictionary/english/bracelet
https://dictionary.cambridge.org/us/dictionary/english/bracelet
you can read that a bracelet is a piece of jewelry that is worn around the wrist or arm.
In this definition, it is important for us now that a bracelet has a circular form like a closed line.
So, the question can be EQUIVALENTLY reformulated in THIS WAY
In how many ways can 7 charms be placed along a circumference of a circle ?
In such problems the placements that obtained one from the other by rotation of a circle by some angle are considered as INDISTINGUISHABLE.
Therefore, with each concrete placements, 6 others that obtained from the original placement by rotation, are considered as EQUIVALENT.
Therefore, the number of all possible placements of 7 charms in a bracelet is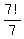 
= 6! = 1*2*3*4*5*6 = 720. ANSWER
It is not 7!, as it would be in linear case !
Solved.
-----------------
The lesson to learn from my post is THIS :
This problem is the same as other classic formulation:
In how many ways 7 people can be sitting around a circular table ?
See the lesson
- Persons sitting around a cicular table
in this site.
