Question 1132628: how many three-digit natural numbers greater than 330 can be formed from the digits 0,1,2,3,4,5 and 6 when each digit can be used only once?
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! how many three-digit natural numbers greater than 330 can be formed from the digits  , , , , , , , , , , and 6 when each digit can be used only once? and 6 when each digit can be used only once?
Case 1: All those between 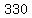 and and 
Choose the first digit  way (as way (as  ) )
That leaves  unchosen digits. unchosen digits.
Choose the second digit any of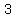 way way  , ,  , , , or , or 
That leaves  unchosen digits unchosen digits
Choose the third digit any of these  ways. ways.
Answer case 1:  ways. ways.
Case 2: Those greater than 
Choose the first digit any of  ways, ways,  , , , or , or 
That leaves  remaining unchosen digits. remaining unchosen digits.
Choose the second digit any of these  remaining unchosen digits. remaining unchosen digits.
That leaves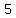 remaining unchosen digits. remaining unchosen digits.
Choose the third digit any of these  remaining unchosen digits. remaining unchosen digits.
Answer to case 2:  ways. ways.
Total for both cases: 
|
|
|