Question 1130264: Suppose four integers are chosen successively at random between 0 and 12, inclusive. Find the probability that:
(Round your answer to four decimal places if necessary.)
a. they are all different?
b. not more than 2 are the same?
Answer by math_helper(2461)   (Show Source):
You can put this solution on YOUR website! I find for this type of problem it is easier to count the number of ways the event(s) of interest
can occur then divide by the total number of possible outcomes.
The number of selections of 4 numbers from the set (0, 1, . . ., 12), with replacement, is  . This will be the denominator in our probability calculation.
Note: Using notation (nCr = n!/((n-r)!r!))
a) There are 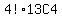 ways to pick 4 unique numbers from the set of 13 (4! because A,B,C,D
and C,B,D,A are the same pick but picked in different order).
P(no matches) =  or about 
b) P(no more than two match) = P(no matches) + P(exactly two match) = 1320/2197 + P(exactly two match)
P(exactly two match) =  or about 0.12016
P(no more than two match) =  or about 
This is probably the answer your teacher is looking for.
I'd like to point out: if {A,B,C,D} are any four unique numbers selected from the set {0,1, . . ., 12} then part (b) addresses A,B,C,D (and its permutations) and A,A,B,C (and its permutations) while the pattern A,A,B,B (and its permutations) are NOT counted. For example, {7,7,11,11} is NOT counted in part (b) even though technically there are only two matching numbers. When I interpret "not more than 2 are the same" I sometimes think {7,7,11,11} should be included.
----
EDITED: Fixed the wording on the paragraph about number of selections of 4 numbers, and added this section:
To include the pattern {A,A,B,B}, add to the above answer:
P(AABB) =  to part (b).
|
|
|
