Question 1127577: Two dice are rolled, find the probabilities of the following events
a.) the sum of the dice is 9
b.) the sum is greater than 10
c.) the sum is less than 6
Found 2 solutions by math_helper, MathLover1:
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are 11 possible outcomes for the sum of two dice (2-12, inclusive):
Sum Number of ways to get this sum
2 1
3 2
4 3
5 4
6 5
7 6
8 5
9 4
10 3
11 2
12 1
a) Pr(sum is 9) = 4/36 = 1/9
b) Pr(sum > 10) = (2+1)/36 = 3/36 = 1/12
c) Pr(sum < 6) = (1+2+3+4)/36 = 10/36 = 5/18
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Two dice are rolled, find the probabilities of the following events:
a.) the sum of the dice is 
b.) the sum is 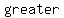 than than 
c.) the sum is 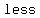 than than 
Solution:
The sample space 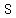 of two dice is shown below. of two dice is shown below.
 = (1,1),(1,2),(1,3),(1,4),(1,5),(1,6) = (1,1),(1,2),(1,3),(1,4),(1,5),(1,6)
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6) ->
a) sum equal to 
Let  be the event "sum equal to be the event "sum equal to  ". There are ". There are  outcomes ((3,6),(4,5),(5,4),(6,3)) which correspond to a sum equal to outcomes ((3,6),(4,5),(5,4),(6,3)) which correspond to a sum equal to  , hence , hence

b)
sum 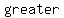 than than 
Let 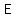 be the event "sum be the event "sum 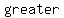 than than  ". There are ". There are  outcomes ((5,6),(6,5),(6,6)) which correspond to a sum outcomes ((5,6),(6,5),(6,6)) which correspond to a sum 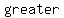 than than  , hence , hence

c.) the sum is less than 
Let  be the event “ the sum is be the event “ the sum is 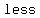 than than  “. There are “. There are  outcomes ((1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,2),(4,1)) which correspond to a sum outcomes ((1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,2),(4,1)) which correspond to a sum 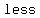 than than  , hence , hence

|
|
|