SOLUTION: How many different signals can be sent up on a flagpole if each signal requires threethree blue and threethree yellow flags and the flags are identical except for​ color?

You have 6 positions, in all :   (3+3 = 6).


Of these 6 positions, you can select 3, where you will place 3 blue flags, by 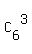  ways =  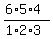= 20 ways.


After that, you just HAVE NO choice where to put yellow flags:

   you have only one opportunity to place them in three places that remained free.



Hence, you have 20 ways and may expose exactly 20 signals, under the given conditions.

We have the set of 6 elements, of which the group of 3 elements are indistinguishable 
and another group of 3 elements are indistinguishable.


The number of all distinguishable arrangements (permutations) of such set is

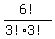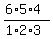     =  = 20,

the same answer.